【题目】如图，已知
平分
， 
于
， 
于
，且
．
（
）求证： 
≌
．
（
）若
， 
， 
，求
的长．
【答案】（
）证明见解析；（
）
．
【解析】试题分析：（1）已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，根据角平分线的性质定理可得CE=CF，再由
，根据HL即可判定△BCE≌△DCF；（2）由Rt△BCE≌△Rt△DCF可得DF=EB，再由HL证明Rt△AFC≌△Rt△AEC，即可得AE=AF，设DF=x，则有9+x=21-x，得x=6，在Rt△CDF中，根据勾股定理求得CF=8，在Rt△AFC中，再运用勾股定理求得AC即可．
试题解析：
（
）证明：∵
平分
， 
于
， 
于
，
∴
， 
， 
，
∵
，
∴
≌
．
（
）由（
）得， 
≌
，
∴
，
∵
与
中，
，
∴
≌
，
∴
，
设
，则有
，得
，
在
中， 
， 
，
∴
，
在
中， 
， 
，
∴
．
字词句篇与同步作文达标系列答案科目：初中数学 来源： 题型：
【题目】已知一次函数y=2x+4
（1）在如图所示的平面直角坐标系中，画出函数的图象；
2）求图象与x轴的交点A的坐标，与y轴交点B的坐标；
（3）在（2）的条件下，求出△AOB的面积；
（4）利用图象直接写出：当y＜0时，x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在宽为20m，长为32m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪．要使草坪的面积为540m2，求道路的宽．
（部分参考数据：322=1024，522=2704，482=2304）
查看答案和解析>>
科目：初中数学 来源： 题型：
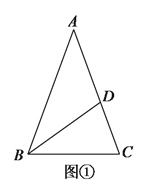
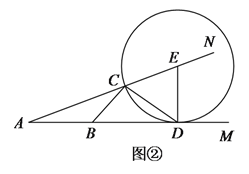
【题目】（
）如图①，在
中，
，点
在
上，且
，求
的度数．
（
）如图②，点
，在射线
上，点
，
在射线
上，且
．
①若
，求的度数．
②若以为圆心，
为半径作弧，与射线
上没有交点（除点外），直接写出的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF，连接AF，BE．
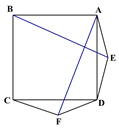
（图1） （图2） （备用图）
（1）请判断：AF与BE的数量关系是_____________，位置关系______________；
（2）如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予证明；
（3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】新农村社区改造中，有一部分楼盘要对外销售，某楼盘共23层，销售价格如下：第八层楼房售价为4000元/米2，从第八层起每上升一层，每平方米的售价提高50元；反之，楼层每下降一层，每平方米的售价降低30元，已知该楼盘每套楼房面积均为120米2．
若购买者一次性付清所有房款，开发商有两种优惠方案：
方案一：降价8%，另外每套楼房赠送a元装修基金；
方案二：降价10%，没有其他赠送．
（1）请写出售价y（元/米2）与楼层x（1≤x≤23，x取整数）之间的函数关系式；
（2）老王要购买第十六层的一套楼房，若他一次性付清购房款，请帮他计算哪种优惠方案更加合算．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一辆客车从甲地开往乙地，一辆轿车从乙地开往甲地，两车同时出发，两车行驶x小时后，记客车离甲地的距离为y1千米，轿车离甲地的距离为y2千米，y1、y2关于x的函数图象如图．
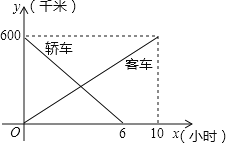
（1）根据图象，直接写出y1、y2关于x的函数关系式；
（2）当两车相遇时，求此时客车行驶的时间；
（3）两车相距200千米时，求客车行驶的时间．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com