练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，△ABC和△关于直线m对称．

    (1)结合图形指出对称点．

    (2)连接A、，直线m与线段AA′有什么关系？

    (3)延长线段AC与A′C′，它们的交点与直线m有怎样的关系？其他对应线段(或其延长线)的交点呢？你发现了什么规律，请叙述出来与同伴交流．

    答案：
    解析：

    　　解：(1)对称点有A和A'，B和B'，C和C'．

    　　(2)连接A、A′，直线m是线段AA′的垂直平分线．

    　　(3)延长线段AC与A′C′，它们的交点在直线m上，其他对应线段(或其延长线)的交点也在直线m上，即若两线段关于直线m对称，且不平行，则它们的交点或它们的延长线的交点在对称轴上．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心。重心有很多美妙的性质，如在关线段比．面积比就有一些“漂亮”结论，利用这些性质可以解决三角形中的若干问题。请你利用重心的概念完成如下问题：

    （1）若O是△ABC的重心（如图1），连结AO并延长交BC于D，证明：；

    （2）若AD是△ABC的一条中线（如图2），O是AD上一点，且满足，试判断O是△ABC的重心吗？如果是，请证明；如果不是，请说明理由；

    （3）若O是△ABC的重心，过O的一条直线分别与AB、AC相交于G、H（均不与△ABC的顶点重合）（如图3），S四边形BCHG．S△AGH分别表示四边形BCHG和△AGH的面积，试探究的最大值。

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：

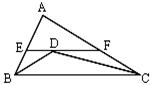
    如图，ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，当∠A的位置及大小变化时，线段EF和BE+CF的大小关

    A. EF>BE+CF   B. EF=BE+CF   C. EF<BE+CF   D. 不能确定 （    ）

    查看答案和解析>>

    同步练习册答案