解:(1)显然∠MPN≠90°,
若∠PMN=90°,则CM=4,
若∠PNM=90°,则PN=3,CN=4,MN=

,
∴CM=

;
(2)(甲)CM•AN的值不确定(显然,CM可以为0,从而CM•AN的值为0);
(乙)CN•AM的值保持不变,且CN•AM=25.
证明如下:
连CP,由已知:∠ACB=90°,AB=10,
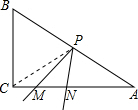
∵点P是AB中点,
∴CP=AP=5.
∴∠PCA=∠PAC=∠MPN.
∴∠PMA=∠CPN.
∴△CPN∽△AMP.
∴
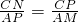
.
∴CN•AM=25.
(3)∵∠MPN=∠A,
∴∠APN+∠ANP=∠APN+∠BPM,
∴∠ANP=∠BPM.
要使△BMP与△ANP相似,
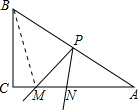
①若∠MBP=∠A,则BM=AM,
又P是AB中点,
∴MP⊥AB,
∴△AMP∽△ABC.
∴AM=

,
从而CM=

;
②若∠BMP=∠A,
则∠BMP=∠MPN,
∴△BMP∽△BAM.

=
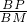
,
∴
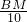
=
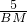
,
∴BM=

.
从而CM=

.
分析:(1)根据已知条件可以确定显然∠MPN≠90°,若∠PMN=90°,根据已知条件可以求出CM=4;若∠PNM=90°,则根据已知条件得到PN=3,CN=4,MN=

,然后就可以求出CM;
(2)甲的CM•AN的值不确定,由于CM可以为0,从而CM•AN的值为0;乙的CN•AM的值保持不变,且CN•AM=25,连CP,根据已知条件可以得到△CPN∽△AMP,然后根据相似三角形的性质即可求出CN•AM=25;
(3)由∠MPN=∠A得到∠APN+∠ANP=∠APN+∠BPM,接着得到∠ANP=∠BPM,要使△BMP与△ANP相似,
①若∠MBP=∠A,则BM=AM,又P是AB中点,可以得到MP⊥AB,从而推出△AMP∽△ABC.然后根据相似三角形的性质即可求解;
②若∠BMP=∠A,则∠BMP=∠MPN,可以得到△BMP∽△BAM,同①可以求出BM,从而求出CM.
点评:此题主要考查了相似三角形的性质与判定及勾股定理的应用,解题时要求学生熟练掌握相似三角形的判定方法才能很好解决问题.

 的两边分别与边AC交于点M、N.
的两边分别与边AC交于点M、N. ,
, ;
;
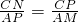 .
.
 ,
, ;
; =
=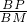 ,
,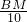 =
=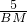 ,
, .
. .
. ,然后就可以求出CM;
,然后就可以求出CM;

 如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )
如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( ) 22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点.
22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点.