
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
【答案】A
【解析】∵∠C=90°,BC=2cm,∠A=30°,
∴AB=4,
由勾股定理得:AC=2![]() ,
,
∵四边形DEFG为矩形,∠C=90,
∴DE=GF=2![]() ,∠C=∠DEF=90°,
,∠C=∠DEF=90°,
∴AC∥DE,
此题有三种情况:
(1)当0<x<2时,AB交DE于H,如图
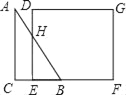
∵DE∥AC,
∴![]() ,
,
即![]() ,
,
解得:EH=![]() x,
x,
所以y=![]()
![]() xx=
xx=![]() x2,
x2,
∵x 、y之间是二次函数,
所以所选答案C错误,答案D错误,
∵a=![]() >0,开口向上;
>0,开口向上;
(2)当2≤x≤6时,如图,
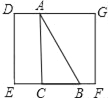
此时y=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
(3)当6<x≤8时,如图,设△ABC的面积是s1,△FNB的面积是s2,
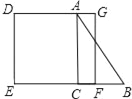
BF=x﹣6,与(1)类同,同法可求FN=![]() X﹣6
X﹣6![]() ,
,
∴y=s1﹣s2,
=![]() ×2×2
×2×2![]() ﹣
﹣![]() ×(x﹣6)×(
×(x﹣6)×(![]() X﹣6
X﹣6![]() ),
),
=﹣![]() x2+6
x2+6![]() x﹣16
x﹣16![]() ,
,
∵﹣![]() <0,
<0,
∴开口向下,
所以答案A正确,答案B错误,
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
(1)试确定这两函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△AOB的面积;
(3)根据图象直接写出反比例函数值大于一次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点M(n,﹣n )在第二象限,过点M的直线y=kx+b(0<k<1)分别交x轴、y轴于点A,B,过点M作MN⊥x轴于点N,则下列点在线段AN的是( )
A. ((k﹣1)n,0) B. ((k+![]() )n,0)) C. (
)n,0)) C. (![]() ,0) D. ((k+1)n,0)
,0) D. ((k+1)n,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
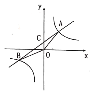
(1)求![]() =______,
=______,![]() =______;
=______;
(2)根据函数图象可知,当![]() 时,
时,![]() 的取值范围是____________.
的取值范围是____________.
(3)求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
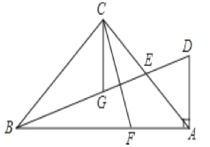
(1)求证:BG=CF;
(2)求证:CF=2DE;
(3)若DE=1,求AD的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com