
����Ŀ��Ϊ��ȫ���˽�ѧ����ѧϰ�������ͥ�Ļ����������ǿѧУ����ͥ����ϵ��÷����ѧ������֯ȫ���ʦ��չ���������һ��������ʦ�����ڰ༶��ȫ��ѧ������ʵ�ؼҷã��˽ÿ��ѧ����ͥ�������Ϣ���ȴ��������ȡ15��ѧ����ͥ����������������������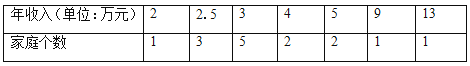
��1������15��ѧ����ͥ�������ƽ��������λ����������
��2������Ϊ�ã�1���е��ĸ�������������15��ѧ����ͥ�������һ��ˮƽ��Ϊ���ʣ����Ҫ˵�����ɣ�
���𰸡�
��1��
��𣺽⣺��15��ѧ����ͥ�������ƽ�����ǣ� ![]() ��Ԫ������15�����ݴ�С�������У����м������3��������λ����3��Ԫ������һ��������3���ִ������ģ���������3��Ԫ��
��Ԫ������15�����ݴ�С�������У����м������3��������λ����3��Ԫ������һ��������3���ִ������ģ���������3��Ԫ��
��2��
�������������15��ѧ����ͥ�������һ��ˮƽ��Ϊ���ʣ���Ϊ3���ֵĴ�����࣬���������ܴ�����ͥ�������һ��ˮƽ��
����������1������ƽ��������λ���������Ķ�����⼴�ɣ���2����ƽ���������������У�ƽ�����ܵ�����ֵ��Ӱ��ϴ������������ܷ�ӳ��ͥ�������һ��ˮƽ��
�����㾫����������Ҫ��������λ�������������֪ʶ�㣬��Ҫ������λ����Ψһ�ģ��������ݵ�����λ���йأ������ܳ�������������ݣ���������һ����Ҳ���ܶ������һ�������������е���������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����⣺��ͼ���ڡ�ABC�У���A=42�㣬��ABC�͡�ACB��ƽ�����ཻ�ڵ�D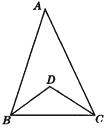
��1�����BDC�Ķ�����
��2���ڣ�1����ȥ����A=42�������������̽����BDC�͡�A֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
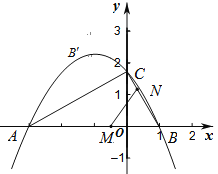
����Ŀ����ͼ����֪��![]() �����κ���
�����κ���![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() ����ͼ�����
����ͼ�����![]() ��
��![]() �ύ����һ��
�ύ����һ��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
��1������κ����Ľ���ʽ��д���������ꣻ
��2������![]() ͬʱ��
ͬʱ��![]() �����������ÿ��2����λ���ȵ��ٶȷֱ���
�����������ÿ��2����λ���ȵ��ٶȷֱ���![]() ��
��![]() �����˶��������˶���ʱ��Ϊ
�����˶��������˶���ʱ��Ϊ![]() �룬������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶�������
�룬������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶�������![]() ����
����![]() ��
��![]() ���ۣ�����
���ۣ�����![]() ǡ�������������ϵ�
ǡ�������������ϵ�![]() ��������
��������![]() ��ֵ����
��ֵ����![]() �����ꣻ
�����ꣻ
��3���ڣ�2���������£�QΪBN���е㣬��̽�����������Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() Ϊ�������������
Ϊ�������������![]() ���ƣ�������ڣ��������
���ƣ�������ڣ��������![]() �����ꣻ��������ڣ���˵������.
�����ꣻ��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1+��2��180�㣬��3����B����DE��BC������������ͬѧ���Ƶ����̩o��������������������Ƶ����ݻ����ݣ� ֤����
�ߡ�1+��2��180����֪����
��1����4 ������
���2����180�㣮
��EH��AB ������
���B����EHC������
�ߡ�3����B����֪��
���3����EHC������
��DE��BC������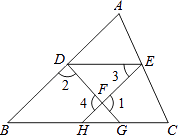
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��һԪ���η���
��һԪ���η���![]() ��
��
��1����֤����������������ȵ�ʵ������
��2���跽�̵�����ʵ�����ֱ�Ϊ![]() ��
�� ![]() ������
������![]() ������
������![]() �ǹ���t�ĺ�������
�ǹ���t�ĺ�������![]() ������������Ľ���ʽ,����������ͼ��
������������Ľ���ʽ,����������ͼ��
��3���۲죨2���еĺ���ͼ��![]() ʱ��д���Ա���
ʱ��д���Ա���![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ֲ������ɳ���������Ŀ��֧�ɣ�ÿ��֧���ֳ���ͬ����Ŀ��С��֧�����ɣ���֧��С��֧������91��ÿ��֧�ɳ�����С��֧��Ŀ�ǣ�������
A.8
B.9
C.10
D.11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. x3+x3=x6 B. 3x3y2��xy2=3x4
C. x3��2x��2=4x5 D. ����3a2��2=6a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���QΪ����ϵ������һ�㣬ijͼ���ϵ����е��ڡ�Q���ڲ������ǵıߣ�����ʱ���ǰѡ�Q����С�ǽ�����ͼ�ε��ӽǣ���ͼ1������ABCD��������OA��OB����ơ�AOBΪ����ABCD���ӽǣ�
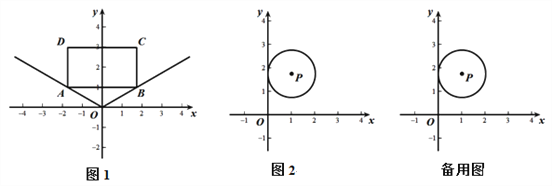
��1����ͼ1������ABCD��A����![]() ��1����B��
��1����B��![]() ��1����C��
��1����C��![]() ��3����D����
��3����D����![]() ��3����ֱ��д���ӽǡ�AOB�Ķ�����
��3����ֱ��д���ӽǡ�AOB�Ķ�����
��2���ڣ�1���������£�������CB����һ��Q��ʹ�þ���ABCD���ӽǡ�AQB=60�������Q�����ꣻ
��3����ͼ2����P�İ뾶Ϊ1����P��1�� ![]() ������Q��x���ϣ��ҡ�P���ӽǡ�EQF�Ķ�������60������Q��a��0������a��ȡֵ��Χ��
������Q��x���ϣ��ҡ�P���ӽǡ�EQF�Ķ�������60������Q��a��0������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P������Ϊ��m��1,m2��2m��3��,���P��ֱ��y����5�������СֵΪ�� ����
A.0.5B.1C.1.5D.2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com