
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求AD:EF的值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)由线段垂直平分线的性质得出GA=GB,GD=GC,由SAS证明△AGD≌△BGC,得出对应边相等即可;
(2)先证出∠AGB=∠DGC,由![]() ,证出△AGB∽△DGC,得出比例式
,证出△AGB∽△DGC,得出比例式![]() ,再证出∠AGD=∠EGF,即可得出△AGD∽△EGF;
,再证出∠AGD=∠EGF,即可得出△AGD∽△EGF;
(3)延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH,由△AGD≌△BGC,得出∠GAD=∠GBC,再求出∠AGB=∠AHB=90°,得出∠AGE=![]() ∠AGB=45°,求出
∠AGB=45°,求出![]() ,由△AGD∽△EGF,即可得出
,由△AGD∽△EGF,即可得出![]() 的值.
的值.
试题解析:(1)证明:∵GE是AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
 ,
,
∴△AGD≌△BGC(SAS),
∴AD=BC;
(2)证明:∵∠AGD=∠BGC,
∴∠AGB=∠DGC,
在△AGB和△DGC中, ![]() ,
,
∴△AGB∽△DGC,
∴![]() ,
,
又∵∠AGE=∠DGF,
∴∠AGD=∠EGF,
∴△AGD∽△EGF;
(3)延长AD交GB于点M,交BC的延长线于点H,如图所示:
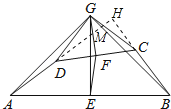
则AH⊥BH,
∵△AGD≌△BGC,
∴∠GAD=∠GBC,
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,
∴∠AGB=∠AHB=90°,
∴∠AGE=![]() ∠AGB=45°,
∠AGB=45°,
∴![]() ,
,
又∵△AGD∽△EGF,
∴![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某个体水果店经营香蕉,每千克进价![]() 元,售价
元,售价![]() 元,10月1日至10月5日经营情况如下表:
元,10月1日至10月5日经营情况如下表:
![]() 若9月30日晚库存为0,则10月1日晚库存______ kg;
若9月30日晚库存为0,则10月1日晚库存______ kg;
![]() 就10月3日这一天的经营情况看,当天是赚钱还是赔钱,规定赚钱为正,则当天赚______ 元;
就10月3日这一天的经营情况看,当天是赚钱还是赔钱,规定赚钱为正,则当天赚______ 元;
![]() 月1日到10月5日该个体户共赚多少钱?
月1日到10月5日该个体户共赚多少钱?
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 |
购进kg | 55 | 45 | 50 | 50 | 50 |
售出 | 44 |
| 38 |
| 51 |
损耗 | 6 | 2 | 12 | 5 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果农种了50棵苹果树,收获时,他把苹果树的产量做了一下统计,得到下表:
质量(千克) | 33 | 34 | 35 | 36 | 38 |
数量(棵) | 10 | 5 | 20 | 10 | 5 |
(1)苹果产量的众数是;中位数是;平均数是;
(2)市场上苹果的销售价为8元/千克,化肥、农药、人工费等共投入资金1000元,则今年该果农纯收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2![]() ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.



(Ⅰ)如图1,求∠DAO的大小及线段DE的长;
(Ⅱ)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3![]() .
.
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com