
【题目】刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点![]() 距离地面的高
距离地面的高![]() 米.
米.![]() 米,当吊臂顶端由
米,当吊臂顶端由![]() 点抬升至
点抬升至![]() 点(吊臂长度不变时),地面
点(吊臂长度不变时),地面![]() 处的重物(大小忽略不计)被吊至
处的重物(大小忽略不计)被吊至![]() 处,紧绷着的吊缆
处,紧绷着的吊缆![]() .且
.且![]() .
.
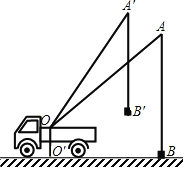
(1)求此重物在水平方向移动的距离及在竖直方向移动的距离;
(2)若这台吊车工作时吊杆最大水平旋转角度为![]() ,吊杆与水平线的倾角可以从
,吊杆与水平线的倾角可以从![]() 转到
转到![]() ,求吊车工作时,工作人员不能站立的区域的面积.
,求吊车工作时,工作人员不能站立的区域的面积.
【答案】(1)3米,![]() 米
米
(2)![]() 平方米
平方米
【解析】
(1)先过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则得出
,则得出![]() ,通过解直角三角形
,通过解直角三角形![]() 和
和![]() 得出
得出![]() 与
与![]() ,从而求出
,从而求出![]() ;先解直角三角形
;先解直角三角形![]() ,得出
,得出![]() ,然后求出
,然后求出![]() ;
;
(2)吊杆端点![]() 最远水平距离为吊杆与水平线的倾角为
最远水平距离为吊杆与水平线的倾角为![]() 时,所以代入数值求解直角三 角形即可求出
时,所以代入数值求解直角三 角形即可求出 ![]() 的长,即吊车工作时工作人员不能站立的区域的半径,由圆的面积的公式即可去求出区域面积.
的长,即吊车工作时工作人员不能站立的区域的半径,由圆的面积的公式即可去求出区域面积.
解:(1)过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]()

根据题意可知![]()
![]()
在![]() 中,
中,![]() ,
,![]()
![]()
![]() ,在
,在![]() 中,
中,
![]() ,
,![]()
![]()
![]()
在![]() 中,
中,
![]()
![]()
![]()
![]()
![]()
![]()
答:此重物在水平方向移动的距离是3米,此重物在竖直方向移动的距离![]() 是
是![]() 米;
米;
(2)当水平距离为吊杆与水平线的倾角为![]() 时,即吊车工作时工作人员不能站立的区域的半径,
时,即吊车工作时工作人员不能站立的区域的半径,
在![]() 中,
中,![]() ,
,
![]() 这台吊车工作时吊杆最大水平旋转角度为
这台吊车工作时吊杆最大水平旋转角度为![]()
![]() 工作人员不能站立的区域的面积为:
工作人员不能站立的区域的面积为:![]() (平方米)
(平方米)


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A点,D点分别在x轴、y轴上,对角线BD∥x轴,反比例函数![]() 的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
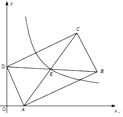
A.16B.20C.32D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .直线
.直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,设直线
是抛物线的顶点,设直线![]() 上方的抛物线上的动点
上方的抛物线上的动点![]() 的横坐标为
的横坐标为![]() .
.
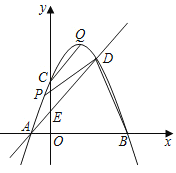
(1)连接![]() ,求证:四边形
,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)连接![]() ,
,![]() ,当
,当![]() 为何值时
为何值时![]() ?
?
(3)在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 为等腰直角三角形?若存在,请求出点
为等腰直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.机场对乘客进行安检不能采用抽样调查
B.一组数据10,11,12,9,8的平均数是10,方差是2
C.“清明时节雨纷纷”是随机事件
D.一组数据6,5,3,5,4的众数是5,中位数是3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在三角形纸片ABC中,∠BAC=78°,AC=10.数学实践课上,小敏用5张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图2所示),并通过上网查到以下几个数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.7.请你帮助她解决下列问题:

(1)∠ABC= °;
(2)求正五边形GHMNC的边GC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,顶点为
,顶点为![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)若![]() 的坐标为
的坐标为![]() ,当
,当![]() 时,二次函数
时,二次函数![]() 有最大值
有最大值![]() ,求
,求![]() 的值;
的值;
(3)直线![]() 与直线
与直线![]() 、直线
、直线![]() 分别相交于
分别相交于![]() 、
、![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() (包含
(包含![]() 、
、![]() 两点)有两个公共点,求
两点)有两个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
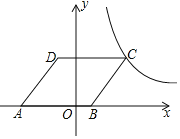
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com