
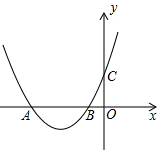
 如图,抛物线y=$\frac{1}{8}$x2+3mx+18m2-m与x轴交于A(x1,0),B(x2,0)两点,且x1≠x2,与y轴交于点C.
如图,抛物线y=$\frac{1}{8}$x2+3mx+18m2-m与x轴交于A(x1,0),B(x2,0)两点,且x1≠x2,与y轴交于点C.分析 (1)由题意△>0,列出不等式即可解决问题.
(2)由OA+OB=3OC,列出方程即可解决问题.
解答 解:(1)由题意△>0,
即(3m)2-4×$\frac{1}{8}$×(18m2-m)=$\frac{1}{2}$m>0,
∴m>0.
(2)∵OA+OB=3OC,
∴-(x1+x2)=24m=3(18m2-m),
解得m=$\frac{1}{2}$或0(舍弃),
∴抛物线的解析式为y=$\frac{1}{8}$x2+$\frac{3}{2}$x+4.
点评 本题考查抛物线与x轴的交点、待定系数法确定函数解析式等知识,解题的关键是学会用转化的思想思考问题,把问题转化为方程解决,属于中考常考题型.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形ABCD中,∠D=60°,E为线段CD上一点,连接BE,将线段BC沿直线BE翻折交对角线AC于点F,连接EF,则∠FEB的角度为30°.
如图,菱形ABCD中,∠D=60°,E为线段CD上一点,连接BE,将线段BC沿直线BE翻折交对角线AC于点F,连接EF,则∠FEB的角度为30°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
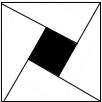 如图,利用四个全等的直角三角形拼成的“赵爽弦图”中,小正方形的面积是1,大正方形的面积是25,直角三角形中较大的锐角为β,那么tanβ=$\frac{4}{3}$.
如图,利用四个全等的直角三角形拼成的“赵爽弦图”中,小正方形的面积是1,大正方形的面积是25,直角三角形中较大的锐角为β,那么tanβ=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com