
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量![]() 与单价
与单价![]() 满足一次函数关系,求出
满足一次函数关系,求出![]() 与
与![]() 的关系式;
的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
科目:初中数学 来源: 题型:
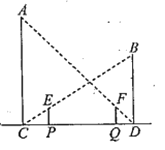
【题目】如图,王乐同学在晩上由路灯![]() 走向路灯
走向路灯![]() .当他行到
.当他行到![]() 处时发现,他往路灯
处时发现,他往路灯![]() 下的影长为2m,且恰好位于路灯
下的影长为2m,且恰好位于路灯![]() 的正下方,接着他又走了
的正下方,接着他又走了![]() 到
到![]() 处,此时他在路灯
处,此时他在路灯![]() 下的影孑恰好位于路灯
下的影孑恰好位于路灯![]() 的正下方(已知王乐身高
的正下方(已知王乐身高![]() ,路灯
,路灯![]() 高
高![]() ).
).
(1)王乐站在![]() 处时,在路灯
处时,在路灯![]() 下的影子是哪条线段?
下的影子是哪条线段?
(2)计算王乐站在![]() 处时,在路灯
处时,在路灯![]() 下的影长;
下的影长;
(3)计算路灯![]() 的高度.
的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
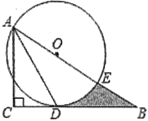
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D,以AB上点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=6,劣弧DE的长为π,求线段BD,BE与劣弧DE所围成的阴影部分的面积(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
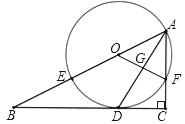
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
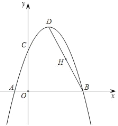
(1)求抛物线的解析式及顶点D的坐标;
(2)在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com