
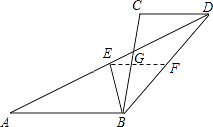
【题目】如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点. 
(1)若BK= ![]() KC,求
KC,求 ![]() 的值;
的值;
(2)连接BE,若BE平分∠ABC,则当AE= ![]() AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=
AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE= ![]() AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.
【答案】
(1)解:∵BK= ![]() KC,
KC,
∴ ![]() =
= ![]() ,
,
又∵CD∥AB,
∴△KCD∽△KBA,
∴ ![]() =
= ![]() =
= ![]()
(2)解:当BE平分∠ABC,AE= ![]() AD时,AB=BC+CD;
AD时,AB=BC+CD;
证明:取BD的中点为F,连接EF交BC于G点,
由中位线定理,得EF∥AB∥CD,
∴G为BC的中点,∠GEB=∠EBA,
又∵∠EBA=∠GBE,
∴∠GEB=∠GBE,
∴EG=BG= ![]() BC,而GF=
BC,而GF= ![]() CD,EF=
CD,EF= ![]() AB,
AB,
∵EF=EG+GF,
即: ![]() AB=
AB= ![]() BC+
BC+ ![]() CD;
CD;
∴AB=BC+CD;
同理,当AE= ![]() AD(n>2)时,EF∥AB,
AD(n>2)时,EF∥AB,
同理可得: ![]() =
= ![]() ,则BG=
,则BG= ![]() BC,则EG=BG=
BC,则EG=BG= ![]() BC,
BC,
![]() =
= ![]() =
= ![]() ,则GF=
,则GF= ![]() CD,
CD,
![]() =
= ![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() CD=
CD= ![]() AB,
AB,
∴BC+CD=(n﹣1)AB,
故当AE= ![]() AD(n>2)时,BC+CD=(n﹣1)AB.
AD(n>2)时,BC+CD=(n﹣1)AB.
【解析】(1)由已知得 ![]() =
= ![]() ,由CD∥AB可证△KCD∽△KBA,利用
,由CD∥AB可证△KCD∽△KBA,利用 ![]() =
= ![]() 求值;(2)AB=BC+CD.作△ABD的中位线,由中位线定理得EF∥AB∥CD,可知G为BC的中点,由平行线及角平分线性质,得∠GEB=∠EBA=∠GBE,则EG=BG=
求值;(2)AB=BC+CD.作△ABD的中位线,由中位线定理得EF∥AB∥CD,可知G为BC的中点,由平行线及角平分线性质,得∠GEB=∠EBA=∠GBE,则EG=BG= ![]() BC,而GF=
BC,而GF= ![]() CD,EF=
CD,EF= ![]() AB,利用EF=EG+GF求线段AB、BC、CD三者之间的数量关系;当AE=
AB,利用EF=EG+GF求线段AB、BC、CD三者之间的数量关系;当AE= ![]() AD(n>2)时,EG=BG=
AD(n>2)时,EG=BG= ![]() BC,而GF=
BC,而GF= ![]() CD,EF=
CD,EF= ![]() AB,EF=EG+GF可得BC+CD=(n﹣1)AB.
AB,EF=EG+GF可得BC+CD=(n﹣1)AB.
【考点精析】掌握角平分线的性质定理和相似三角形的判定与性质是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )

A. ![]() a2 B.
a2 B. ![]() a2 C.
a2 C. ![]() a2 D.
a2 D. ![]() a
a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的伴随方程,这个根在数轴上对应的点该不等式组的伴随点.
(1)在方程①![]() ,②
,②![]() ,③
,③![]() 中,不等式组
中,不等式组![]() 的伴随方程是 ;(填序号)
的伴随方程是 ;(填序号)
(2)如图,M、N都是关于![]() 的不等式组
的不等式组![]() 的伴随点,求
的伴随点,求![]() 的取值范围.
的取值范围.
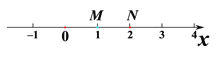
(3)不等式组![]() 的伴随方程的根有且只有2个整数,求
的伴随方程的根有且只有2个整数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,其中真命题的个数是( )
①平面直角坐标系内的点与实数对一一对应;
②内错角相等;
③平行于同一条直线的两条直线互相平行;
④对顶角相等
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8.过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的T处,折痕为MN.当点T在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,则线段AT长度的最大值与最小值之和为(计算结果不取近似值).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店推出一种优惠卡,每张卡售价为50元,凭卡购书可享受8折优惠,小明同学到该书店购书,他先买购书卡再凭卡付款,结果省了10元。若此次小明不买卡直接购书,则他需要付款( )
A.380元B.360元C.340元D.300元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com