
【题目】问题提出:
(1)如图①,若正方形![]() 的边长为6,点
的边长为6,点![]() 分别为边
分别为边![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() ;
;
问题探究:
(2)如图②,![]() ,
,![]() 是等腰直角三角形,顶点
是等腰直角三角形,顶点![]() 分别在
分别在![]() 的两边上,试说明点
的两边上,试说明点![]() 在
在![]() 的平分线上;
的平分线上;
问题解决:
(3)如图③,![]() ,
,![]() 是等边三角形,顶点
是等边三角形,顶点![]() 分别在
分别在![]() 的两边上,点
的两边上,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() ,求
,求![]() 的最小值.
的最小值.

【答案】(1)3![]() ;(2)见解析;(3)3
;(2)见解析;(3)3![]() .
.
【解析】
(1)先证明△AEH≌△BFE≌△CGF≌△DHG,可得出四边形GHEF是菱形,再根据全等三角形角之间的关系,又可得出菱形的一个角是直角,那么就可得出四边形GHEF是正方形.过点O分别作OM⊥AB于点M,ON⊥BC于点N,根据AAS易得△EOM≌△FON,得出OC=OD,根据角平分线的判定定理可得OB平分∠ABC,根据BO=![]() BD可得出结果..
BD可得出结果..
(2)过点O分别作OC⊥AP于点C,OD⊥PN于点D,证明△EOC≌△BOD,得出OC=OD,根据角平分线的判定定理可得出结果.
(3)过点O分别作OC⊥AP于点C,OD⊥PN于点D,同(2)中证法可得点O在∠MPN的平分线上,连接PO,过点Q作QO′⊥PO于点O′,则QO′即为QO的最小值,在Rt△PQO′中求出QO′的值即可.
解:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵HA=EB=FC=GD,
∴AE=BF=CG=DH,
∴△AEH≌△BFE≌△CGF≌△DHG,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∵△DHG≌△AEH,
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴四边形EFGH是正方形.
∴EO=FO,∠EOF=90°.
过点O分别作OM⊥AB于点M,ON⊥BC于点N,
根据AAS易得△EOM≌△FON,
∴MO=NO,
∴BO平分∠ABC,
∴BO=![]() BD=
BD=![]() BC=3
BC=3![]() .
.
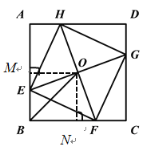
图①
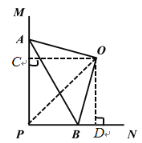
(2)过点O分别作OC⊥AP于点C,OD⊥PN于点D,
∵∠APB=90°,
∴∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
又AO=BO,∠ACO=∠ODB,
∴△AOC≌△BOD(AAS),
∴CO=DO,
又OC⊥PM,OD⊥PN,
∴点![]() 在
在![]() 的平分线上.
的平分线上.
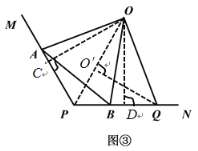
(3) 过点O分别作OC⊥PM于点C,OD⊥PN于点D,同(2)中证法可得点O在∠MPN的平分线上,连接PO,过点Q作QO′⊥PO于点O′
∵OP为∠MPN的平分线,
∴∠OPN=60°,
又PQ=6,∴PO′=3,
∴QO′=3![]() .
.
即QO的最小值为3![]() .
.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
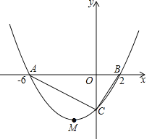
【题目】如图所示,抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求抛物线的函数解析式;
求抛物线的函数解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 能否在抛物线第三象限的图象上找到一点
能否在抛物线第三象限的图象上找到一点![]() ,使
,使![]() 的面积最大?若能,请求出点
的面积最大?若能,请求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船从点A处出发,先航行至位于点A的南偏西15°且点A相距100km的点B处,再航行至位于点A的南偏东75°且与点B相距200km的点C处.
(1)求点C与点A的距离(精确到1km);
(2)确定点C相对于点A的方向.
(参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,点
,点![]() 为
为![]() 三条角平分线的交点,
三条角平分线的交点,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() ,
,![]() ,则点
,则点![]() 到三边
到三边![]() 、
、![]() 、
、![]() 的距离为( )
的距离为( )
A. 2cm,2cm,2cm B. 3cm,3cm,3cm
C. 4cm,4cm,4cm D. 2cm,3cm,5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,把△ABC沿直线DE折叠,使△ADE与△BDE重合.
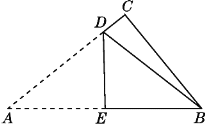
(1)若∠A=35°,则∠CBD的度数为________;
(2)若AC=8,BC=6,求AD的长;
(3)当AB=m(m>0),△ABC的面积为m+1时,求△BCD的周长.(用含m的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
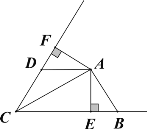
【题目】如图,AC平分∠BCD,AB=AD, AE⊥BC于E,AF⊥CD于F
(1)若∠ABE= 50° ,求∠CDA的度数.
(2)若AE=4,BE=2,CD=6,求四边形AECD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
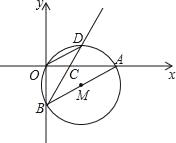
【题目】如图,直角坐标系中,⊙M经过原点O(0,0),点A(![]() ,0)与点B(0,﹣1),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CBO.
,0)与点B(0,﹣1),点D在劣弧OA上,连接BD交x轴于点C,且∠COD=∠CBO.
(1)请直接写出⊙M的直径,并求证BD平分∠ABO;
(2)在线段BD的延长线上寻找一点E,使得直线AE恰好与⊙M相切,求此时点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com