
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为____ _____.
),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为____ _____.

【答案】![]()
【解析】
试题分析:
作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,求出AD,再求出DN、CN,根据勾股定理求出CD,即可得出答案.
试题解析:
解:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,
则此时PA+PC的值最小.
∵DP=PA,
∴PA+PC=PD+PC=CD.
∵B(3,![]() ),
),
∴AB=![]() ,OA=3,∠B=60°.
,OA=3,∠B=60°.
由勾股定理得:OB=2![]() .
.
由三角形面积公式得:![]() ×OA×AB=
×OA×AB=![]() ×OB×AM,
×OB×AM,
∴AM=![]() .
.
∴AD=2×![]() =3.
=3.
∵∠AMB=90°,∠B=60°,
∴∠BAM=30°.
∵∠BAO=90°,
∴∠OAM=60°.
∵DN⊥OA,
∴∠NDA=30°.
∴AN=![]() AD=
AD=![]() .
.
由勾股定理得:DN=![]() .
.
∵C(1,0),
∴CN=3-1-![]() =
=![]() .
.
在Rt△DNC中,由勾股定理得:DC=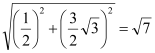 .
.
∴PA+PC的最小值是![]() .
.



 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
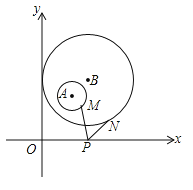
【题目】如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图□ABCD的对角线AC、BD交于点O ,AE平分∠BAD交BC于点E ,且∠ADC=600,AB=![]() BC ,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC ,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=![]() BC 成立的个数有( )
BC 成立的个数有( )
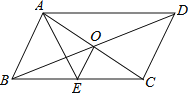
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
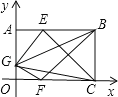
【题目】如图,已知OABC是一个长方形,其中顶点A,B的坐标分别为(0,a)和(9,a),点E在AB上,且AE=AG,点F在OC上,且OF=![]() OC,点G在OA上,且使△GEC的面积为20,△GFB的面积为16,试求a的值.
OC,点G在OA上,且使△GEC的面积为20,△GFB的面积为16,试求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com