
已知:如下图,在△ABC中D、E分别是AC、AB上的点,BD、CE交于O.

给出下列四个条件①∠EBO=∠DCO ②∠BEO=∠CDO ③BE=CD ④OB=OC.
(1)上述四个条件中,哪两个条件可以判别△ABC是等腰三角形(用序号写出所有情形)?
(2)选择(1)中的一种情形,证明△ABC是等腰三角形.
科目:初中数学 来源:新课标3维同步训练与评价·数学·九年级·上 题型:044
将下面证明中每一步的理由写在括号内.
已知:如下图,AB=AC、DB=DC、AD的延长线交BC于E.
求证:AE⊥BC

证明:在△ABD和△ACD中
∵AB=AC( )
DB=DC( )
AD=AD( )
∴△ABD≌△ACD( )
∴∠BAD=∠CAD( )
即AE为∠BAC平分线
∴AE⊥BC( )
查看答案和解析>>
科目:初中数学 来源:2001~2002学年度第二学期教学目标检测 初二数学 题型:047
已知:如下图,点E、F在DC上,DF=EC,AD=BC,∠D=∠C.
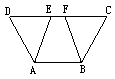
求证:△AED≌△BFC.
查看答案和解析>>
科目:初中数学 来源:2001~2002学年度第二学期教学目标检测 初二数学 题型:047
已知:如下图,在△ABC中,AB=AC,D、E分别在AB、AC上,M、N在DE上,AM=AN,且AM⊥MC,AN⊥NB.

求证:∠MAD=∠NAE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com