
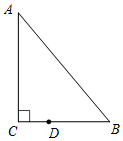 如图,Rt△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把线段BD 绕着点D逆时针旋转α(0<α<180)度后,如果点B恰好落在Rt△ABC的边上,那么α=70°或120°.
如图,Rt△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把线段BD 绕着点D逆时针旋转α(0<α<180)度后,如果点B恰好落在Rt△ABC的边上,那么α=70°或120°. 分析 设旋转后点B的对应点为B′,当B′在线段AB上时,连接B′D,由旋转的性质可得BD=B′D,利用等腰三角形的性质结合三角形内角和定理可求得∠BDB′;当点B′在线段AC上时,连接B′D,在Rt△B′CD中可求得∠CDB′,则可求得旋转角,可求得答案.
解答 解:
设旋转后点B的对应点为B′,
①当B′在线段AB上时,连接B′D,如图1,
由旋转性质可得BD=B′D,
∴∠DB′B=∠B=55°,
∴α=∠BDB′=180°-55°-55°=70°;
②当点B′在线段AC上时,连接B′D,如图2,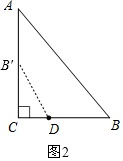
由旋转性质可得BD=B′D,
∵BD=2CD,
∴B′D=2CD,
∴sin∠CB′D=$\frac{CD}{B′D}$=$\frac{1}{2}$,
∴∠CB′D=30°,
∴∠BDB′=90°+30°=120°;
综上可知旋转角α为70°或120°,
故答案为:70°或120°.
点评 本题主要考查旋转的性质,掌握旋转前后对应线段相等是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图所示,已知数轴上两点A、B对应的数分别为-2、4,点P为数轴上一动点.
如图所示,已知数轴上两点A、B对应的数分别为-2、4,点P为数轴上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.12×106 | B. | 3.12×105 | C. | 31.2×105 | D. | 0.312×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 38x-15=42x+5 | B. | 38x+15=42x-5 | C. | 42x+38x=15+5 | D. | 42x-38x=15-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com