
解:(1)①x=0时,y=1,y=0时,2x+1=0,解得x=-

,
所以,直线y=2x+1经过点(0,1)(-

,0),
②当x=0时,y=3,当y=0时,-2x+3=0,解得x=

,
所以,直线y=-2x+3经过点(0,3)(

,0),
③当x=0时,y=-1,当y=0时,

x-1=0,解得x=2,
所以,直线y=

x-1经过点(0,-1)(2,0),
④当x=0时,y=2,当y=0时,-

x+2=0,解得x=4,
所以,直线y=-

x+2经过点(0,2)(4,0),
作图如图所示;
(2)由图可知,y=2x+1与y=-

x+2垂直,y=-2x+3与y=

x-1垂直,
∵2×(-

)=-1,-2×

=-1,
∴猜想当k
1•k
2=-1时,y=k
1x+b
1,y=k
2x+b
2的图象相互垂直;
故答案为:k
1•k
2=-1;
(3)根据(2)的结论,
∵正比例函数y=

x的图象和⊙P相切于点A,
∴直线AP的k值等于-2,
所以,设直线AP的解析式为y=-2x+b,
∵OP=3,
∴点P的坐标为(3,0),
∴-2×3+b=0,
解得b=6,
∴直线AP的解析式为y=-2x+6,
联立

,
解得

,
所以,OA=

=


,
AP=

=
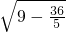
=


,
⊙P的面积=π•AP
2=π•(


)
2=

π.
分析:(1)分别求出直线与坐标轴的交点,然后根据两点确定一条直线,利用两点法作出直线图象即可;
(2)结合图象根据互相垂直的两直线解析式的k值解答;
(3)根据(2)的结论求出直线AP的k值,然后求出直线AP的解析式,与OA的解析式联立求解得到点A的坐标,再利用勾股定理求出OA的长度,再次利用勾股定理求出PA的长度,然后根据圆的面积公式列式计算即可得解.
点评:本题是对一次函数的综合考查,主要涉及利用两点法作一次函数图象,联立两直线解析式求直线的交点,勾股定理的应用,是综合题,但难度不大,读懂题目信息,准确作出图形是解题的关键.

 我们知道两个一次函数y=k1x+b1,y=k2x+b2,当k1=k2时,这两个一次函数的图象相互平行,那么两个一次函数的图象什么情况下相互垂直呢?下面我们就来探索.
我们知道两个一次函数y=k1x+b1,y=k2x+b2,当k1=k2时,这两个一次函数的图象相互平行,那么两个一次函数的图象什么情况下相互垂直呢?下面我们就来探索. x-1,y=-
x-1,y=- x+2的图象;
x+2的图象; x的图象和⊙P相切于点A,点P在x轴上,OP=3厘米,求⊙P的面积.
x的图象和⊙P相切于点A,点P在x轴上,OP=3厘米,求⊙P的面积. 解:(1)①x=0时,y=1,y=0时,2x+1=0,解得x=-
解:(1)①x=0时,y=1,y=0时,2x+1=0,解得x=- ,
, ,0),
,0), ,
, ,0),
,0), x-1=0,解得x=2,
x-1=0,解得x=2, x-1经过点(0,-1)(2,0),
x-1经过点(0,-1)(2,0), x+2=0,解得x=4,
x+2=0,解得x=4, x+2经过点(0,2)(4,0),
x+2经过点(0,2)(4,0), x+2垂直,y=-2x+3与y=
x+2垂直,y=-2x+3与y= x-1垂直,
x-1垂直, )=-1,-2×
)=-1,-2× =-1,
=-1, x的图象和⊙P相切于点A,
x的图象和⊙P相切于点A, ,
, ,
, =
=
 ,
, =
=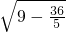 =
=
 ,
,
 )2=
)2= π.
π.

 (2013•镇江)通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=
(2013•镇江)通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=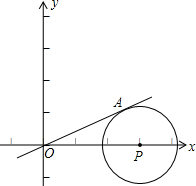 我们知道两个一次函数y=k1x+b1,y=k2x+b2,当k1=k2时,这两个一次函数的图象相互平行,那么两个一次函数的图象什么情况下相互垂直呢?下面我们就来探索.
我们知道两个一次函数y=k1x+b1,y=k2x+b2,当k1=k2时,这两个一次函数的图象相互平行,那么两个一次函数的图象什么情况下相互垂直呢?下面我们就来探索. x-1,y=-
x-1,y=- x+2的图象;
x+2的图象; x的图象和⊙P相切于点A,点P在x轴上,OP=3厘米,求⊙P的面积.
x的图象和⊙P相切于点A,点P在x轴上,OP=3厘米,求⊙P的面积.