
难(12分)如图,在等腰梯形ABCE中, BC∥AE且![]() =
=![]() ,以点E为坐标原点建立平面直角坐标系,若将梯形ABCD沿AC折叠, 使点B恰好落在x轴上点D位置,过C、D两点的直线与y轴交于点E.
,以点E为坐标原点建立平面直角坐标系,若将梯形ABCD沿AC折叠, 使点B恰好落在x轴上点D位置,过C、D两点的直线与y轴交于点E.
(1)试判断四边形ABCD是怎样的特殊四边形,并说明你的理由;
(2)如果∠![]() =60°,
=60°,![]() =
=![]()
![]() ,那么在
,那么在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使以
,使以![]() 、
、![]() 、
、
![]() 为顶点的三角形构成等腰三角形,若存在,请求出所有可能的
为顶点的三角形构成等腰三角形,若存在,请求出所有可能的![]() 点坐标,若不存在,请说明理由;
点坐标,若不存在,请说明理由;
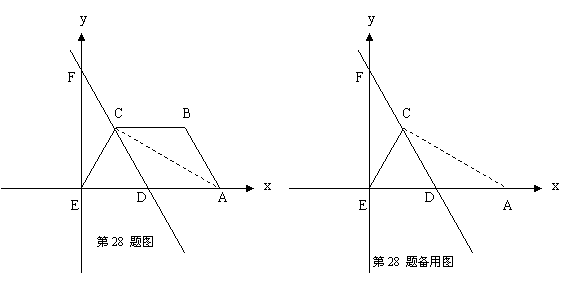
(3)在(2)的条件下,若将![]()
![]() 沿
沿![]() 轴正方向以1
轴正方向以1![]() /
/![]() 的速度平移到点
的速度平移到点![]() 与点
与点![]() 重合时为止,设
重合时为止,设![]()
![]() 在平移过程中与
在平移过程中与![]()
![]() 重合部分的面积为
重合部分的面积为![]() ,平移的时间为
,平移的时间为![]() 秒,试求出
秒,试求出![]() 与
与![]() 之间的函数关系式及自变量范围,并求出何时
之间的函数关系式及自变量范围,并求出何时![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
解:(1)四边形ABCD为菱形------- 1′
理由如下:因为点B和点D关于z直线AC对称,所以AB=AD;BC=DC.
由AB=BC得:AB=BC=DA=AB,
所以四边形ABCD为菱形. ------- 2′(其他方法参照给分)
⑵∵四边形ABCD为菱形 ∴![]() ∥
∥![]() ∴
∴![]() ∴
∴![]() 为等边三角形 ∴
为等边三角形 ∴![]() 在
在![]() 中,
中,![]()
![]()
① 以![]() 为腰,
为腰,![]() 点坐标为
点坐标为![]() 、
、![]() 、
、![]()
②以![]() 为底,
为底,![]() 点坐标为
点坐标为
② 综上所述,![]() 点坐标为
点坐标为![]() 、
、![]() 、
、![]() 、
、 ………………………………6分
………………………………6分

⑶①当![]()
![]() ≤
≤![]() ≤
≤![]()
![]() 时,
时,![]() =
=![]() ∴当
∴当![]() =
=![]()
![]() 时,
时,![]() 有最大值=
有最大值=![]()
………………………………8分
②当![]()
![]() ≤
≤![]() ≤2
≤2![]() 时
时
,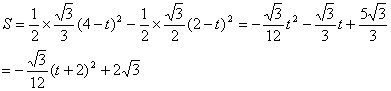
∴当![]() 1s时,
1s时,![]() 有最大值=
有最大值=![]() ………………………………10分
………………………………10分
③ 当![]()
![]() ≤
≤![]() ≤4
≤4![]() 时,
时,![]()
∴当![]() 2时,
2时,![]() 有最大值=
有最大值=![]()
综上所述,当![]() =
=![]()
![]() 时,
时,![]() 有最大值=
有最大值=![]() ………………………………12分
………………………………12分


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年江西省九江市十一中中考数学二模试卷(徐丽)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com