
【题目】(探究函数![]() 的图象与性质)
的图象与性质)
(1)函数![]() 的自变量x的取值范围是________;
的自变量x的取值范围是________;
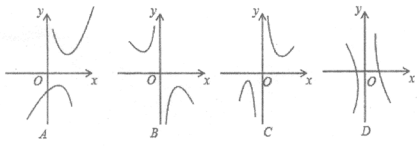
(2)下列四个函数图象中,函数![]() 的图象大致是_______;
的图象大致是_______;
(3)对于函数![]() ,求当x>0时,y的取值范围。请将下面求解此问题的过程补充完整:
,求当x>0时,y的取值范围。请将下面求解此问题的过程补充完整:
解:因为x>0,所以![]()
![]() _________。
_________。
因为![]() ,所以y________。
,所以y________。
(拓展运用)
(4)若函数![]() ,则y的取值范围是_______________________。
,则y的取值范围是_______________________。
【答案】(1)x≠0;(2)C;(3)6,y≥6;(4)y≤-11或y≥1.
【解析】
(1)由![]() 中x≠0,即可得出函数y=x+
中x≠0,即可得出函数y=x+![]() 的自变量x的取值范围;
的自变量x的取值范围;
(2)由x≠0可排除A选项,再由y与x同号,可知函数y=x+![]() 的图象在第一、三象限,由此即可得出结论;
的图象在第一、三象限,由此即可得出结论;
(3)根据用配方法求y值的范围的过程补充完整解题过程,即可得出结论;
(4)将![]() 变成y=x+
变成y=x+![]() -5,由(3)的结论可得出y=x+
-5,由(3)的结论可得出y=x+![]() 中y的取值范围为y≤-6或y≥6,在此基础上减去5即可得出结论.
中y的取值范围为y≤-6或y≥6,在此基础上减去5即可得出结论.
解:(1)∵在y=x+![]() 中,x≠0,
中,x≠0,
∴x的取值范围是x≠0.
故答案为:x≠0;
(2)∵x≠0,
∴A中图象不符合题意;
∵当x>0时,x+![]() >0,
>0,
当x<0时,x+![]() <0,
<0,
∴函数y=x+![]() 的图象在第一、三象限,
的图象在第一、三象限,
∴B、D中图象不符合题意,
故选C.
(3)解:∵x>0,
∴y=x+![]() ,
,![]() 6,
6,
∵![]() ,
,
∴y≥6.
故答案为:6;≥6.
(4)![]() =x+
=x+![]() -5.
-5.
由(3)可知:当x>0时,x+![]() ≥6;
≥6;
当x<0时,x+![]() ≤-6.
≤-6.
∴y=x+![]() -5≥6-5=1,y=x+
-5≥6-5=1,y=x+![]() -5≤-6-5=-11.
-5≤-6-5=-11.
y的取值范围是y≤-11或y≥1.
故答案为:(1)x≠0;(2)C;(3)6,y≥6;(4)y≤-11或y≥1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图,根据图象回答下列问题:
的图象如图,根据图象回答下列问题:
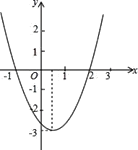
(1)写出方程![]() 的两个根;
的两个根;
(2)写出不等式![]() 的解集;
的解集;
(3)写出不等式![]() 的解集;
的解集;
(4)如果方程![]() 无实数根,求
无实数根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
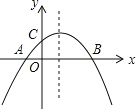
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC;则下列结论:①abc<0;②![]() >0;③ac-b+1=0;④OAOB=-
>0;③ac-b+1=0;④OAOB=-![]() .其中正确的结论( )
.其中正确的结论( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BC·AB=AC2,那么称线段AB被点C黄金分割。
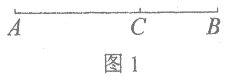
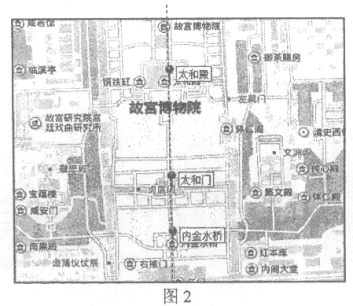
为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域。如图2,在我国古代紫禁城的中轴线上,太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割,已知太和殿到内金水桥的距离约为100丈,求太和门到太和殿之间的距离(![]() 的近似值取2.2)。
的近似值取2.2)。
查看答案和解析>>
科目:初中数学 来源: 题型:
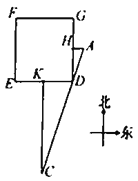
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.
查看答案和解析>>
科目:初中数学 来源: 题型:
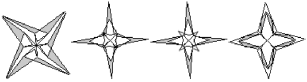
【题目】下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
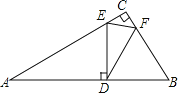
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
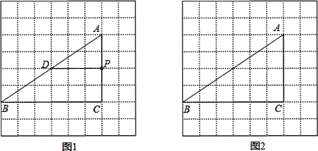
【题目】在![]() 中,
中,![]() ,
,
(1)如图![]() ,
,![]() 是
是![]() 上的点,过点
上的点,过点![]() 作直线截
作直线截![]() ,使截得的三角形与
,使截得的三角形与![]() 相似.例如:过点
相似.例如:过点![]() 作
作![]() 交
交![]() 于
于![]() ,则截得的
,则截得的![]() 与
与![]() 相似.请你在图中画出所有满足条件的直线.
相似.请你在图中画出所有满足条件的直线.
(2)如图![]() ,
,![]() 是
是![]() 上异于点
上异于点![]() ,
,![]() 的动点,过点
的动点,过点![]() 作直线截
作直线截![]() ,使截得的三角形与
,使截得的三角形与![]() 相似,直接写出满足条件的直线的条数.(不要求画出具体的直线)
相似,直接写出满足条件的直线的条数.(不要求画出具体的直线)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com