
已知![]() 与
与![]() 是反比例函数
是反比例函数![]() 图象上的两个点.
图象上的两个点.
(1)求![]() 的值;
的值;
(2)若点![]() ,则在反比例函数
,则在反比例函数![]() 图象上是否存在点
图象上是否存在点![]() ,使得以
,使得以![]() 四点为顶点的四边形为梯形?若存在,求出点
四点为顶点的四边形为梯形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

解:(1)由![]() ,得
,得![]() ,因此
,因此![]() .
.
(2)如图1,作![]() 轴,
轴,![]() 为垂足,则
为垂足,则![]() ,
,![]() ,
,![]() ,因此
,因此![]() .
.
由于点![]() 与点
与点![]() 的横坐标相同,因此
的横坐标相同,因此![]() 轴,从而
轴,从而![]() .
.
当![]() 为底时,由于过点
为底时,由于过点![]() 且平行于
且平行于![]() 的直线与双曲线只有一个公共点
的直线与双曲线只有一个公共点![]() ,
,
故不符题意.
当![]() 为底时,过点
为底时,过点![]() 作
作![]() 的平行线,交双曲线于点
的平行线,交双曲线于点![]() ,
,
过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴的平行线,交于点
轴的平行线,交于点![]() .
.
由于![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
由点![]() ,得点
,得点![]() .
.
因此![]()
解之得![]() (
(![]() 舍去),因此点
舍去),因此点 .
.
此时![]() ,与
,与![]() 的长度不等,故四边形
的长度不等,故四边形![]() 是梯形.
是梯形.

如图2,当![]() 为底时,过点
为底时,过点![]() 作
作![]() 的平行线,与双曲线在第一象限内的交点为
的平行线,与双曲线在第一象限内的交点为![]() .
.
由于![]() ,因此
,因此![]() ,从而
,从而![]() .作
.作![]() 轴,
轴,![]() 为垂足,
为垂足,
则![]() ,设
,设![]() ,则
,则![]() ,
,![]()
由点![]() ,得点
,得点![]() ,
,
因此![]()
解之得![]() (
(![]() 舍去),因此点
舍去),因此点![]() .
.
此时![]() ,与
,与![]() 的长度不相等,故四边形
的长度不相等,故四边形![]() 是梯形.
是梯形.
如图3,当过点![]() 作
作![]() 的平行线,与双曲线在第三象限内的交点为
的平行线,与双曲线在第三象限内的交点为![]() 时,
时,
同理可得,点![]() ,四边形
,四边形![]() 是梯形.
是梯形.
综上所述,函数![]() 图象上存在点
图象上存在点![]() ,使得以
,使得以![]() 四点为顶点的四边形为梯形,点
四点为顶点的四边形为梯形,点![]() 的坐标为:
的坐标为: 或
或![]() 或
或![]() .
.



科目:初中数学 来源:2007年初中毕业升学考试(江苏常州卷)数学(带解析) 题型:解答题
已知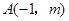 与
与 是反比例函数
是反比例函数 图象上的两个点.
图象上的两个点.
(1)求 的值;
的值;
(2)若点 ,则在反比例函数
,则在反比例函数 图象上是否存在点
图象上是否存在点 ,使得以
,使得以 四点为顶点的四边形为梯形?若存在,求出点
四点为顶点的四边形为梯形?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年浙江省瑞安市初中毕业生学业考试适应性测试数学试卷(带解析) 题型:解答题
已知 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。
(1)求 的值;
的值;
(2)求直线AB的函数解析式;
(3)若点 ,点
,点 是反比例函数
是反比例函数 图象上的一点,如果以
图象上的一点,如果以 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 的坐标(能求出一个点即可)。
的坐标(能求出一个点即可)。
查看答案和解析>>
科目:初中数学 来源:2013届河南省郑州市第四中学九年级中招模拟数学试卷(带解析) 题型:解答题
已知 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。
(1)求 的值;
的值;
(2)求直线AB的函数解析式;
(3)若点 ,点
,点 是反比例函数
是反比例函数 图象上的一点,如果以
图象上的一点,如果以 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 的坐标(能求出一个点即可)
的坐标(能求出一个点即可)
|
查看答案和解析>>
科目:初中数学 来源:2012-2013学年河南省郑州市九年级中招模拟数学试卷(解析版) 题型:解答题
已知 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。

(1)求 的值;
的值;
(2)求直线AB的函数解析式;
(3)若点 ,点
,点 是反比例函数
是反比例函数 图象上的一点,如果以
图象上的一点,如果以 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 的坐标(能求出一个点即可)
的坐标(能求出一个点即可)
|
。
查看答案和解析>>
科目:初中数学 来源:2013年浙江省瑞安市毕业生学业考试适应性测试数学试卷(解析版) 题型:解答题
已知 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。

(1)求 的值;
的值;
(2)求直线AB的函数解析式;
(3)若点 ,点
,点 是反比例函数
是反比例函数 图象上的一点,如果以
图象上的一点,如果以 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 的坐标(能求出一个点即可)。
的坐标(能求出一个点即可)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com