
【题目】如图,已知在Rt△ABC中,![]() ,以BC为直径作
,以BC为直径作![]() 交AB于点E,D为AC边的中点,连接OD、DE,
交AB于点E,D为AC边的中点,连接OD、DE,
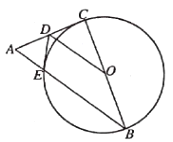
(1)求证:DE是![]() 的切线.
的切线.
(2)填空:①若![]() ,
,![]() ,则
,则![]() 的半径长是__________.
的半径长是__________.
②当∠A=__________时,四边形OCDE是正方形.
【答案】(1)证明见解析;(2)① ![]() ;② 45°
;② 45°
【解析】
(1)连接OE、CE,由圆周角定理得出∠BEC=90°,则∠AEC=90°,由直角三角形斜边上的中线性质得出AD=CD=DE,由等腰三角形的性质得出∠DEC=∠DCE,∠OCE=∠OEC,证出∠OED=90°,即可得出结论;
(2)①由勾股定理求出CE=2![]() ,证△OCE∽△DAE,得出比例式,求出OC的长即可;
,证△OCE∽△DAE,得出比例式,求出OC的长即可;
②证△ABC是等腰直角三角形,得出∠ABC=45°,证四边形OCDE是矩形,由OC=OE,即可得出四边形OCDE是正方形.
(1)证明:连接OE、CE,如图所示:
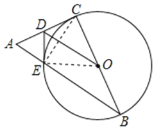
∵BC是⊙O的直径,
∴∠BEC=90°,
∴∠AEC=90°,
∵D是AC的中点,
∴DE=![]() AC=AD=CD,
AC=AD=CD,
∴∠DEC=∠DCE,
∵OC=OE,
∴∠OCE=∠OEC,
∵∠ACB=90°,
∴∠DEC+∠OEC=∠DCE+∠OCE=∠ACB=90°,
∴∠OED=90°,即OE⊥DE,
∵E为⊙O上的点,
∴DE是⊙O的切线;
(2)解:①∵AC=3,
∴AD=DE=![]() AC=
AC=![]() ,
,
∵∠AEC=90°,
∴![]() ,
,
∵∠BEC=90°,
∴∠CBE+∠OCE=90°,
∵∠ACB=90°,
∴∠CBE+∠DAE=90°,
∴∠OCE=∠DAE,
∵AD=DE,OC=OE,
∴∠OCE=∠OEC=∠DAE=∠DEA,
∴△OCE∽△DAE,
∴![]() ,
,
即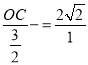 ,
,
解得:OC=3![]() ,
,
故答案为:3![]() ;
;
②当∠A=45°时,四边形OCDE是正方形;理由如下:
∵∠A=45°,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
∵OB=OE,
∴∠OBE=∠OEB=45°,
∴∠COE=∠OBE+∠OEB=45°+45°=90°,
∵∠ACB=90°,∠OED=90°,
∴四边形OCDE是矩形,
∵OC=OE,
∴四边形OCDE是正方形;
故答案为:45°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
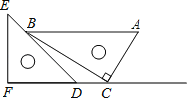
【题目】三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=![]() +
+![]() =1.
=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(1)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立;
(2)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①ac<0,②b﹣2a<0,③b2﹣4ac<0,④a﹣b+c<0,正确的是( )
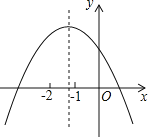
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+2的图象与x轴相交于点A(﹣1,0)、B(4,0),与y轴相交于点C.

(1)求该函数的表达式;
(2)点P为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC.
①求线段PQ的最大值;
②若以点P、C、Q为顶点的三角形与△ABC相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
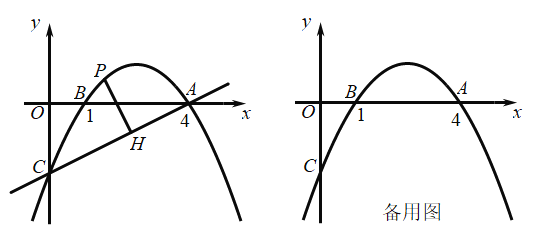
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新冠疫情防控期间,某医疗器械商业集团新进了40台A型电子体温测量仪,60台B型电子体温测量仪,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种测量仪每台的利润(元)如下表:
A型 | B型 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店![]() 台A型测量仪,集团卖出这100台测量仪的总利润为
台A型测量仪,集团卖出这100台测量仪的总利润为![]() (元).
(元).
(1)求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围:
的取值范围:
(2)为了促销,集团决定仅对甲连锁店的A型测量仪每台让利![]() 元销售,其他的销售利润不变,并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润,问该集团应该如何设计调配方案,使总利润达到最大?
元销售,其他的销售利润不变,并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润,问该集团应该如何设计调配方案,使总利润达到最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
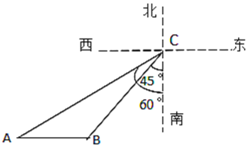
【题目】如图所示,在某海域,一艘指挥船在![]() 处收到渔船在
处收到渔船在![]() 处发出的求救信号,经确定,遇险抛锚的渔船所在的
处发出的求救信号,经确定,遇险抛锚的渔船所在的![]() 处位于
处位于![]() 处的南偏西45°方向上,且
处的南偏西45°方向上,且![]() 海里;指挥船搜索发现,在
海里;指挥船搜索发现,在![]() 处的南偏西60°方向上有一艘海监船
处的南偏西60°方向上有一艘海监船![]() ,恰好位于
,恰好位于![]() 处的正西方向.于是命令海监船
处的正西方向.于是命令海监船![]() 前往搜救,已知海监船
前往搜救,已知海监船![]() 的航行速度为30海里/小时,问渔船在
的航行速度为30海里/小时,问渔船在![]() 处需要等待多长时间才能得到海监船
处需要等待多长时间才能得到海监船![]() 的救援?(参考数据:
的救援?(参考数据:![]() 、
、![]() 、
、![]() 结果精确到0.1小时)
结果精确到0.1小时)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
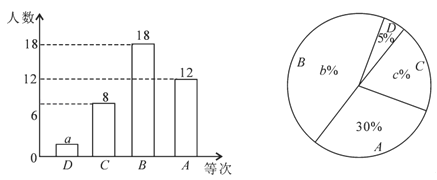
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com