
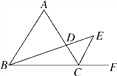
【题目】如图,△ABC是等边三角形,CE是∠ACB的外角平分线,点D在AC上,连接BD并延长交CE于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长.
【答案】(1)详见解析;(2)3![]() .
.
【解析】试题分析:(1)根据等边三角形的性质可得∠BAC=∠ACB=60°,∠ACF=120°,再根据角平分线的性质可得∠ACE=60°,再结合对顶角∠ADB=∠CDE,即可证得结果;
(2)作BM⊥AC于点M,根据等边三角形的性质可得AM=CM=3,BM=AB·sin60°=![]() ,由AD=2CD可得CD=2,AD=4,MD=1,在Rt△BDM中,根据勾股定理可求得BD的长,再根据△ABD∽△CED结合相似三角形的性质可求的ED的长,即可求得结果.
,由AD=2CD可得CD=2,AD=4,MD=1,在Rt△BDM中,根据勾股定理可求得BD的长,再根据△ABD∽△CED结合相似三角形的性质可求的ED的长,即可求得结果.
(1)∵△ABC是等边三角形
∴∠BAC=∠ACB=60°,∠ACF=120°
∵CE是外角平分线
∴∠ACE=60°
∴∠BAC=∠ACE
又∵∠ADB=∠CDE
∴△ABD∽△CED;
(2)作BM⊥AC于点M,AC=AB=6
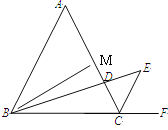
∴AM=CM=3,BM=AB·sin60°=![]()
∵AD=2CD,
∴CD=2,AD=4,MD=1
在Rt△BDM中,BD=![]() =
=![]()
由(1)△ABD∽△CED得, ![]() ,
, ![]() ,
,
∴ED=![]() ,
,
∴BE=BD+ED=![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.

(1)求单摆的长度;
(2)求从点A摆动到点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
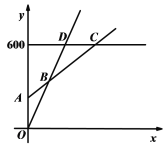
【题目】某水上乐园普通票价20元/张,假期为了促销,新推出两种优惠卡:贵宾卡售价600元/张,每次凭卡不再收费;会员卡售价200元/张,每次凭卡另收10元.暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出假期选择会员卡、普通票消费时,y与x之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C、D的坐标,并直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,![]() 和
和![]() 是等腰直接角三角形,
是等腰直接角三角形,![]() ,点
,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() 恰好是
恰好是![]() 中点,连接
中点,连接![]() .
.
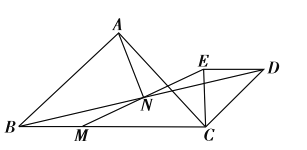
(1)求证:![]() ;
;
(2)连接AM、AE,请探究AN与EN的位置关系与数量关系。
①写出AN与EM:位置关系___;数量关系___;
②请证明上述结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算a![]() b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,则(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,则a=0.
b=0,则a=0.
其中正确结论的序号是 (填上你认为所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织![]() 名同学和
名同学和![]() 名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为
名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为![]() 人/辆,小客车载客量为
人/辆,小客车载客量为![]() 人/辆
人/辆
(1)学校准备租用![]() 辆客车,有几种租车方案?
辆客车,有几种租车方案?
(2)在(1)的条件下,若大客车租金为![]() 元/辆,小客车租金为
元/辆,小客车租金为![]() 元/辆,哪种租车方案最省钱?
元/辆,哪种租车方案最省钱?
(3)学校临时增加![]() 名学生和
名学生和![]() 名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有
名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有![]() 名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有
名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有![]() 人,请你帮助设计租车方案
人,请你帮助设计租车方案
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com