
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴的交点坐标为
轴的交点坐标为![]() 和
和![]() .
.
(1)求![]() 和
和![]() (用
(用![]() 的代数式表示);
的代数式表示);
(2)若在自变量![]() 的值满足
的值满足![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 的最大值为1,求
的最大值为1,求![]() 的值;
的值;
(3)已知点![]() 和点
和点![]() .若二次函数
.若二次函数![]() 的图象与线段
的图象与线段![]() 有两个不同的交点,直接写出
有两个不同的交点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() 和
和![]() ;(3)
;(3)![]() 的取值范围为
的取值范围为![]() .
.
【解析】
(1)二次函数![]() 的图象与
的图象与![]() 轴的交点坐标为
轴的交点坐标为![]() 和
和![]() ,可以看成方程
,可以看成方程![]() 的两个实数根为
的两个实数根为![]() ,
,![]() ,利用根与系数的关系进行求解即可;
,利用根与系数的关系进行求解即可;
(2)二次函数图象开口向下,对称轴为![]() ,分3种情况进行讨论,当
,分3种情况进行讨论,当![]() 、
、 ![]() 、
、![]() 时, 根据二次函数的图像和性质进行求解即可;
时, 根据二次函数的图像和性质进行求解即可;
(3)取临界点,当点A,点B在二次函数![]() 上时,求出m的值,即可求得m的取值范围.
上时,求出m的值,即可求得m的取值范围.
(1)由题意可知,方程![]() 的两个实数根为
的两个实数根为![]() ,
,![]() .
.
∴![]() .
.
∵![]() .
.
(2)由题意可知,二次函数图象开口向下,顶点坐标为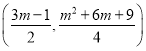 .
.
①当![]() ,即
,即![]() 时,
时,
在自变量![]() 的值满足
的值满足![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 随
随![]() 的增大而减小.
的增大而减小.
故当![]() 时,
时,![]() 为最大值.
为最大值.
∴![]() ,解得
,解得![]() 和
和![]() ,
,![]() ,
,![]() 都不合题意,舍去.
都不合题意,舍去.
②当![]() ,即
,即![]() 时,
时,![]() 为最大值,
为最大值,
∴![]() ,解得
,解得![]() ,
,![]() ,
,![]() 不合题意,舍去.
不合题意,舍去.
③当![]() ,即
,即![]() 时,
时,
在自变量![]() 的值满足
的值满足![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 随
随![]() 的增大而增大.
的增大而增大.
故当![]() 时,
时,![]() 为最大值.
为最大值.
∴![]() ,解得
,解得![]() 和
和![]() ,
,![]() 不合题意,舍去.
不合题意,舍去.
综上所述,![]() 和
和![]() .
.
(3)当点![]() 在二次函数
在二次函数![]() 上时,代入得,
上时,代入得,
![]() ,代入
,代入![]() ;
;![]() 得
得
![]() ,
,
当点![]() 在二次函数
在二次函数![]() 上时,代入得,
上时,代入得,
![]() ,代入
,代入![]() ;
;![]() 得
得
![]() ,
,
∵二次函数![]() 的图象与线段
的图象与线段![]() 有两个不同的交点
有两个不同的交点
∴![]() .
.


科目:初中数学 来源: 题型:
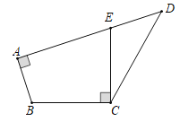
【题目】如图,ABCD中,∠A=45°,连接BD,且BD⊥AD,点E、点F分别是AB、CD上的点,连接EF交BD于点O,且EF⊥CD,BE=DF=1.
(1)求EF的长;
(2)直接写出ABCD的面积 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:
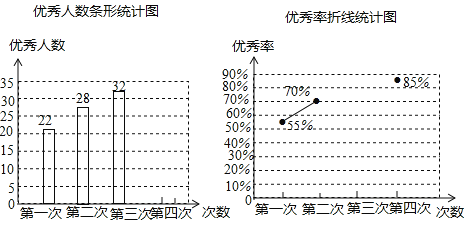
(1)求该班总人数;
(2)根据计算,请你补全两个统计图;
(3)已知该班甲同学四次训练成绩为85,95,85,95,乙同学四次成绩分别为85,90,95,90,现需从甲、乙两同学中选派一名同学参加校级比赛,你认为应该选派哪位同学并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,一块四边形纸板剪去![]() ,得到四边形
,得到四边形![]() ,测得
,测得![]() ,
,![]() ,
,![]() .能否在四边形纸板
.能否在四边形纸板![]() 上只剪一刀,使剪下的三角形与
上只剪一刀,使剪下的三角形与![]() 全等?请说明理由.
全等?请说明理由.
(2)我市某学校八年级同学乘坐大巴车去长江青少年素质教育实践基地参加综合实践活动.1号车出发4分钟后,2号车才出发,结果两车同时到达.已知素质教育基地距离该校18千米,2号车的平均速度是1车的平均速度的![]() 倍.请你就“1号车”提出一个用分式方程解决的问题,并写出解题过程.
倍.请你就“1号车”提出一个用分式方程解决的问题,并写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]()
![]() 过点
过点![]() ,顶点
,顶点![]() 在第三象限,
在第三象限,![]() ,
,![]() 是抛物线的对称轴
是抛物线的对称轴![]() 上的两点,且
上的两点,且![]() ,在直线
,在直线![]() 左侧以
左侧以![]() 为边作正方形
为边作正方形![]() ,点
,点![]() 恰好在抛物线上.
恰好在抛物线上.
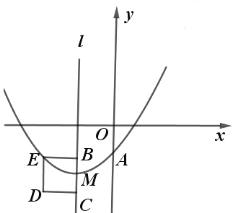
(1)用含![]() 的式子表示
的式子表示![]() ;
;
(2)求证:点![]() 和点
和点![]() 关于直线
关于直线![]() 对称;
对称;
(3)判断直线![]() 和直线
和直线![]() (
(![]() 是常数,且
是常数,且![]() )的交点是否在抛物线上,并说明理由.
)的交点是否在抛物线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年,我省中考体育分值增加到
年,我省中考体育分值增加到![]() 分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
成绩 |
|
|
|
|
|
等级 |
|
|
|
|
|
百分比 |
|
|
|
|
|
(1)求样本容量及表格中的![]() 和
和![]() 的值
的值
(2)求扇形统计图中![]() 等级所对的圆心角度数,并补全统计图.
等级所对的圆心角度数,并补全统计图.
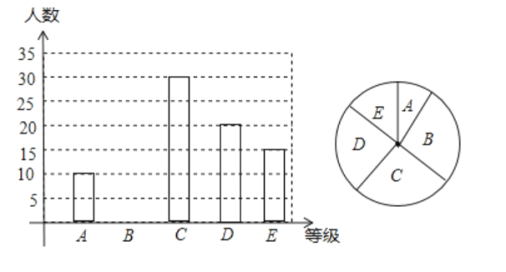
(3)我校![]() 年级共有女生
年级共有女生![]() 人.若女生八百米成绩的达标成绩为
人.若女生八百米成绩的达标成绩为![]() 分,我校九年级女生八百米成绩达标的人数有多少?
分,我校九年级女生八百米成绩达标的人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击疫情,人人有责,某校成立教师志愿者分队,共分宣传、测温、清理(主要厨余垃圾清理)、统计(师生疫情信息统计)四组,为了解教师对这四个小组的参与意愿情况调查,对教师进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表.
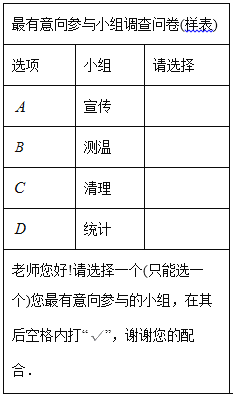
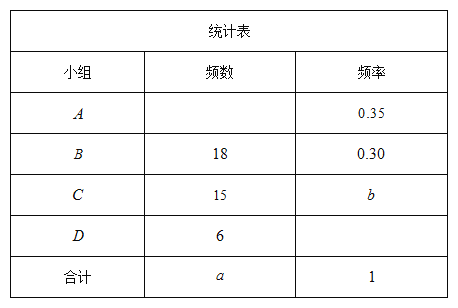
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() _ ,b=_ ;
_ ,b=_ ;
(2)根据调查结果,请你估计该市![]() 名教师中最有意向参与清理小组的人数;
名教师中最有意向参与清理小组的人数;
(3)王老师和李老师选择参与小组,若他们每人从![]() 四个小组中随机选取一个,请用画树状图或列表格的方法,求两人恰好选中同一个的概率.
四个小组中随机选取一个,请用画树状图或列表格的方法,求两人恰好选中同一个的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于x3﹣(n2+1)x+n这类特殊的代数式可以按下面的方法分解因式:
x3﹣(n2+1)x+n=x3﹣n2x﹣x+n=x(x2﹣n2)﹣(x﹣n)=x(x﹣n)(x+n)﹣(x﹣n)=(x﹣n)(x2+nx﹣1).
理解运用:如果x3﹣(n2+1)x+n=0,那么(x﹣n)(x2+nx﹣1)=0,即有x﹣n=0或x2+nx﹣1=0,
因此,方程x﹣n=0和x2+nx﹣1=0的所有解就是方程x3﹣(n2+1)x+n=0的解.
解决问题:求方程x3﹣5x+2=0的解为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com