
 如图所示,是一个上肢力量健身器示意图.配重A受到的重力为350N,其底面积为5×10-2m2.B、C都是定滑轮,D是动滑轮;杠杆EH可绕O点在竖直平面内转动,OE=3OH.小明受到的重力为500N,当他通过细绳在H点分别施加竖直向下的拉力T1、T2时,杠杆两次都在水平位置平衡,小明对地面的压力分别为F1、F2,配重A受到的拉力分别为FA1、FA2,配重A对地面的压强分别为p1、p2,且两次A对地面的压强相差2×103Pa.已知F1:F2=4:3,p1:p2=3:2.杠杆EH和细绳的质量及滑轮组装置的摩擦力均忽略不计.求:
如图所示,是一个上肢力量健身器示意图.配重A受到的重力为350N,其底面积为5×10-2m2.B、C都是定滑轮,D是动滑轮;杠杆EH可绕O点在竖直平面内转动,OE=3OH.小明受到的重力为500N,当他通过细绳在H点分别施加竖直向下的拉力T1、T2时,杠杆两次都在水平位置平衡,小明对地面的压力分别为F1、F2,配重A受到的拉力分别为FA1、FA2,配重A对地面的压强分别为p1、p2,且两次A对地面的压强相差2×103Pa.已知F1:F2=4:3,p1:p2=3:2.杠杆EH和细绳的质量及滑轮组装置的摩擦力均忽略不计.求: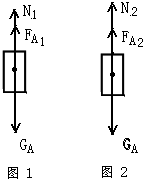

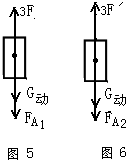
 (FA1+G动)------------⑤
(FA1+G动)------------⑤ (FA2+G动)-----------⑥
(FA2+G动)-----------⑥
 (F绳+G动)=
(F绳+G动)= (350N+50N)=
(350N+50N)= ,
, =
=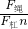 =
=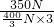 =87.5%.
=87.5%.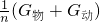 求出杠杆对动滑轮向上的拉力;最后根据η=
求出杠杆对动滑轮向上的拉力;最后根据η= =
=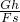 =
=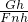 =
= 求出此时滑轮组的机械效率η.
求出此时滑轮组的机械效率η.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中物理 来源: 题型:
 (2011?门头沟区一模)如图所示,是一个上肢力量健身器示意图.配重A的质量为40kg,其底面积为100cm2.B、C、D都是定滑轮,E是动滑轮.杠杆GH可绕O点在竖直平面内转动,OG:OH=2:3.小勇通过细绳在H点施加竖直向下的拉力F1时,配重A受到的拉力为FA1,配重A对地面的压强为2×104Pa;他通过细绳在H点施加竖直向下的拉力F2时,配重A受到的拉力为FA2,配重A对地面的压强为3×104Pa.杠杆两次都在水平位置平衡,杠杆GH和细绳的质量及滑轮组装置的摩擦力均忽略不计,已知F1:F2=9:5,g取10N/kg.求:
(2011?门头沟区一模)如图所示,是一个上肢力量健身器示意图.配重A的质量为40kg,其底面积为100cm2.B、C、D都是定滑轮,E是动滑轮.杠杆GH可绕O点在竖直平面内转动,OG:OH=2:3.小勇通过细绳在H点施加竖直向下的拉力F1时,配重A受到的拉力为FA1,配重A对地面的压强为2×104Pa;他通过细绳在H点施加竖直向下的拉力F2时,配重A受到的拉力为FA2,配重A对地面的压强为3×104Pa.杠杆两次都在水平位置平衡,杠杆GH和细绳的质量及滑轮组装置的摩擦力均忽略不计,已知F1:F2=9:5,g取10N/kg.求:查看答案和解析>>
科目:初中物理 来源: 题型:
 (2009?宣武区一模)如图所示,是一个上肢力量健身器示意图.配重A受到的重力为350N,其底面积为5×10-2m2.B、C都是定滑轮,D是动滑轮;杠杆EH可绕O点在竖直平面内转动,OE=3OH.小明受到的重力为500N,当他通过细绳在H点分别施加竖直向下的拉力T1、T2时,杠杆两次都在水平位置平衡,小明对地面的压力分别为F1、F2,配重A受到的拉力分别为FA1、FA2,配重A对地面的压强分别为p1、p2,且两次A对地面的压强相差2×103Pa.已知F1:F2=4:3,p1:p2=3:2.杠杆EH和细绳的质量及滑轮组装置的摩擦力均忽略不计.求:
(2009?宣武区一模)如图所示,是一个上肢力量健身器示意图.配重A受到的重力为350N,其底面积为5×10-2m2.B、C都是定滑轮,D是动滑轮;杠杆EH可绕O点在竖直平面内转动,OE=3OH.小明受到的重力为500N,当他通过细绳在H点分别施加竖直向下的拉力T1、T2时,杠杆两次都在水平位置平衡,小明对地面的压力分别为F1、F2,配重A受到的拉力分别为FA1、FA2,配重A对地面的压强分别为p1、p2,且两次A对地面的压强相差2×103Pa.已知F1:F2=4:3,p1:p2=3:2.杠杆EH和细绳的质量及滑轮组装置的摩擦力均忽略不计.求:查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,是一个上肢力量健身器示意图.配重A的质量为40kg,其底面积为100cm2.重为500N的小勇通过细绳施加竖直向上的拉力F1时,配重A对地面的压强为2×104Pa,人对地面的压强为P1;他通过细绳施加竖直向上的拉力F2时,配重A对地面的压强为3×104Pa,人对地面的压强为P2.滑轮组装置的摩擦力忽略不计,已知P1:P2=5:4,g取10N/kg.求:
如图所示,是一个上肢力量健身器示意图.配重A的质量为40kg,其底面积为100cm2.重为500N的小勇通过细绳施加竖直向上的拉力F1时,配重A对地面的压强为2×104Pa,人对地面的压强为P1;他通过细绳施加竖直向上的拉力F2时,配重A对地面的压强为3×104Pa,人对地面的压强为P2.滑轮组装置的摩擦力忽略不计,已知P1:P2=5:4,g取10N/kg.求:查看答案和解析>>
科目:初中物理 来源: 题型:
 (2011?大兴区二模)如图所示,是一个上肢力量健身器示意图.配重A受到的重力为1200N,配重A的上方连有一根弹簧测力计D,可以显示所受的拉力大小,但当它所受拉力在0~2500N范围内时,其形变可以忽略不计.B是动滑轮,C是定滑轮;杠杆EH可绕O点在竖直平面内转动,OE:OH=1:6.小阳受到的重力为600N,他通过细绳在H点施加竖直向下的拉力为T1时,杠杆在水平位置平衡,小阳对地面的压力为F1,配重A受到绳子的拉力为FA1,配重A上方的弹簧测力计D显示受到的拉力FD1为2×103N;小阳通过细绳在H点施加竖直向下的拉力为T2时,杠杆仍在水平位置平衡,小阳对地面的压力为F2,配重A受到绳子的拉力为FA2,配重A上方的弹簧测力计D显示受到的拉力FD2为2.3×103N.已知F1:F2=7:5.(杠杆EH、弹簧D和绳的质量以及滑轮与轴的摩擦均忽略不计).求:
(2011?大兴区二模)如图所示,是一个上肢力量健身器示意图.配重A受到的重力为1200N,配重A的上方连有一根弹簧测力计D,可以显示所受的拉力大小,但当它所受拉力在0~2500N范围内时,其形变可以忽略不计.B是动滑轮,C是定滑轮;杠杆EH可绕O点在竖直平面内转动,OE:OH=1:6.小阳受到的重力为600N,他通过细绳在H点施加竖直向下的拉力为T1时,杠杆在水平位置平衡,小阳对地面的压力为F1,配重A受到绳子的拉力为FA1,配重A上方的弹簧测力计D显示受到的拉力FD1为2×103N;小阳通过细绳在H点施加竖直向下的拉力为T2时,杠杆仍在水平位置平衡,小阳对地面的压力为F2,配重A受到绳子的拉力为FA2,配重A上方的弹簧测力计D显示受到的拉力FD2为2.3×103N.已知F1:F2=7:5.(杠杆EH、弹簧D和绳的质量以及滑轮与轴的摩擦均忽略不计).求:查看答案和解析>>
科目:初中物理 来源:2011年北京市门头沟区中考一模物理试卷(解析版) 题型:计算题
如图所示,是一个上肢力量健身器示意图。配重A的质量为40kg,其底面积为100cm2。B、C、D都是定滑轮,E是动滑轮。杠杆GH可绕O点在竖直平面内转动,OG∶OH =2∶3。小勇通过细绳在H点施加竖直向下的拉力F1时,配重A受到的拉力为FA1,配重A对地面的压强为2×104Pa;他通过细绳在H点施加竖直向下的拉力F2时,配重A受到的拉力为FA2,配重A对地面的压强为3×104Pa.杠杆两次都在水平位置平衡,杠杆GH和细绳的质量及滑轮组装置的摩擦力均忽略不计,已知F1∶F2=9∶5, g取10N/kg。求:

(1) 拉力FA2;
(2) 动滑轮的重力G动 ;
(3) 小勇对细绳的拉力F1的大小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com