
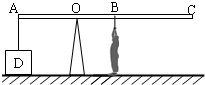
 如图所示的装置,O为杠杆AC的支点,OA:OC=1:2,在杠杆的A点挂一边长为0.2m的立方体D,在杠杆上B点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p1为7000Pa,A点受到向下的拉力为F1?;在杠杆上C点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p2为6000Pa,A点受到向下的拉力为F2?,OB:BC=1:2,杠杆和绳的质量忽略不计.
如图所示的装置,O为杠杆AC的支点,OA:OC=1:2,在杠杆的A点挂一边长为0.2m的立方体D,在杠杆上B点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p1为7000Pa,A点受到向下的拉力为F1?;在杠杆上C点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p2为6000Pa,A点受到向下的拉力为F2?,OB:BC=1:2,杠杆和绳的质量忽略不计.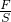 ,
, F,----------①
F,----------① F,-------------------②
F,-------------------②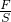 ,
, 得:
得: F:2F=1:3,
F:2F=1:3, F
F (GD-240N)
(GD-240N) F3′=
F3′= ×300N=150N.
×300N=150N.

科目:初中物理 来源: 题型:
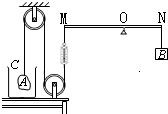 如图所示的装置,O为杠杆的支点,在杠杆上挂有重为60N的重物B,杠杆的左端通过细绳(绳的中间串一个弹簧测力计)跨过定滑轮悬挂着重物A处于静止状态,此时弹簧测力计的示数为40N,杠杆处于水平位置平衡.保持M点位置不动,向容器C中缓慢注水至A完全浸没在水中,测力计示数变为20N.托起容器C,使A接触容器的底部,弹簧测力计的示数逐渐减为10N,同时移动物体B的悬挂点,使杠杆仍在水平位置平衡.若已知容器的底面积为200cm2,杠杆、弹簧测力计、细绳和滑轮的质量以及一切摩擦均可忽略不计,水的密度ρ=1.0×103kg/m3,取g=10N/kg.则根据以上数据可知判断错误的是( )
如图所示的装置,O为杠杆的支点,在杠杆上挂有重为60N的重物B,杠杆的左端通过细绳(绳的中间串一个弹簧测力计)跨过定滑轮悬挂着重物A处于静止状态,此时弹簧测力计的示数为40N,杠杆处于水平位置平衡.保持M点位置不动,向容器C中缓慢注水至A完全浸没在水中,测力计示数变为20N.托起容器C,使A接触容器的底部,弹簧测力计的示数逐渐减为10N,同时移动物体B的悬挂点,使杠杆仍在水平位置平衡.若已知容器的底面积为200cm2,杠杆、弹簧测力计、细绳和滑轮的质量以及一切摩擦均可忽略不计,水的密度ρ=1.0×103kg/m3,取g=10N/kg.则根据以上数据可知判断错误的是( )| A、物体A的体积为2×103cm3 | ||
| B、物体A的密度为2×103kg/m3 | ||
C、物体B的悬挂点应向左移动的距离为杠杆长度的
| ||
| D、若将物体A从容器中取出,取出前后容器底部受水的压强的变化量为100Pa |
查看答案和解析>>
科目:初中物理 来源: 题型:
 (2008?海淀区二模)如图所示的装置,O为杠杆的支点,在杠杆上挂有重为60N的重物B,杠杆的左端通过细绳(绳的中间串一个弹簧测力计)跨过定滑轮悬吊着重物A处于静止状态,此时弹簧测力计的示数为40N,杠杆处于水平位置.现向容器C中缓慢注水,使A浸没,测力计示数变为20N.托起水杯,使A接触容器的底部,弹簧测力计的示数逐渐减为10N,同时移动物体B的悬挂点,使杠杆仍在水平位置平衡.若已知容器的底面积为200cm2,杠杆、弹簧测力计、细绳和滑轮的质量以及一切摩擦均可忽略不计,水的密度ρ=1.0×103kg/m3,取g=10N/kg.则根据以上数据可知( )
(2008?海淀区二模)如图所示的装置,O为杠杆的支点,在杠杆上挂有重为60N的重物B,杠杆的左端通过细绳(绳的中间串一个弹簧测力计)跨过定滑轮悬吊着重物A处于静止状态,此时弹簧测力计的示数为40N,杠杆处于水平位置.现向容器C中缓慢注水,使A浸没,测力计示数变为20N.托起水杯,使A接触容器的底部,弹簧测力计的示数逐渐减为10N,同时移动物体B的悬挂点,使杠杆仍在水平位置平衡.若已知容器的底面积为200cm2,杠杆、弹簧测力计、细绳和滑轮的质量以及一切摩擦均可忽略不计,水的密度ρ=1.0×103kg/m3,取g=10N/kg.则根据以上数据可知( )查看答案和解析>>
科目:初中物理 来源: 题型:
 (2008?丰台区一模)如图所示的装置,O为杠杆AC的支点,OA:OC=1:2,在杠杆的A点挂一边长为0.2m的立方体D,在杠杆上B点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p1为7000Pa,A点受到向下的拉力为F1?;在杠杆上C点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p2为6000Pa,A点受到向下的拉力为F2?,OB:BC=1:2,杠杆和绳的质量忽略不计.
(2008?丰台区一模)如图所示的装置,O为杠杆AC的支点,OA:OC=1:2,在杠杆的A点挂一边长为0.2m的立方体D,在杠杆上B点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p1为7000Pa,A点受到向下的拉力为F1?;在杠杆上C点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p2为6000Pa,A点受到向下的拉力为F2?,OB:BC=1:2,杠杆和绳的质量忽略不计.查看答案和解析>>
科目:初中物理 来源:《第12章 简单机械》2011年单元测试卷(头沟区王平中学)(解析版) 题型:选择题


查看答案和解析>>
科目:初中物理 来源:2008年北京市丰台区中考物理一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com