
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,其前9项和为63.
,其前9项和为63.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)将数列![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行“交叉排列”,得到一个新的数列:
放在前面”的要求进行“交叉排列”,得到一个新的数列:![]() ,求这个新数列的前
,求这个新数列的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)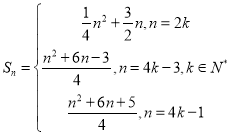
【解析】
试题分析:(1)由已知得数列![]() 是等差数列,从而易得
是等差数列,从而易得![]() ,也即得
,也即得![]() ,利用
,利用![]() 求得
求得![]() ,再求得
,再求得![]() 可得数列
可得数列![]() 通项,利用已知
通项,利用已知![]() 可得
可得![]() 是等差数列,由等差数列的基本量法可求得
是等差数列,由等差数列的基本量法可求得![]() ;(2)代入
;(2)代入![]() 得
得![]() ,变形后得
,变形后得![]() ,从而易求得和
,从而易求得和![]() ,于是有
,于是有![]() ,只要求得
,只要求得![]() 的最大值即可得
的最大值即可得![]() 的最小值,从而得
的最小值,从而得![]() 的范围,研究
的范围,研究![]() 的单调性可得;(3)根据新数列的构造方法,在求新数列的前
的单调性可得;(3)根据新数列的构造方法,在求新数列的前![]() 项和
项和![]() 时,对
时,对![]() 分类:
分类:![]() ,
,![]() 和
和![]() 三类,可求解.
三类,可求解.
试题解析:(1)∵![]() ,∴数列
,∴数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,
的等差数列,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
又![]() ,∴
,∴![]() .
.
∵![]() ,∴数列
,∴数列![]() 是等差数列,
是等差数列,
设![]() 的前
的前![]() 项和为
项和为![]() ,∵
,∵![]() 且
且![]() ,
,
∴![]() ,∴
,∴![]() 的公差为
的公差为![]()
(2)由(1)知![]() ,
,
∴![]()
![]() ,
,
∴![]()
设![]() ,则
,则![]() ,
,
∴数列![]() 为递增数列,
为递增数列,
∴![]() ,
,
∵对任意正整数![]() ,都有
,都有![]() 恒成立,∴
恒成立,∴![]() .
.
(3)数列![]() 的前
的前![]() 项和
项和![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,
,
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ,
,
特别地,当![]() 时,
时,![]() 也符合上式;
也符合上式;
③当![]() 时,
时,![]() .
.
综上: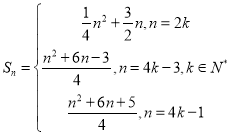


科目:高中数学 来源: 题型:
【题目】现行的个税法修正案规定:个税免征额由原来的2000元提高到3500元,并给出了新的个人所得税税率表:
全月应纳税所得额 | 税率 |
不超过1500元的部分 | 3% |
超过1500元至4500元的部分 | 10% |
超过4500元至9000元的部分 | 20% |
超过9000元至35000元的部分 | 25% |
…… | … |
例如某人的月工资收入为5000元,那么他应纳个人所得税为:![]() (元).
(元).
(Ⅰ)若甲的月工资收入为6000元,求甲应纳的个人收的税;
(Ⅱ)设乙的月工资收入为![]() 元,应纳个人所得税为
元,应纳个人所得税为![]() 元,求
元,求![]() 关于
关于![]() 的函数;
的函数;
(Ⅲ)若丙某月应纳的个人所得税为1000元,给出丙的月工资收入.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某种书籍的成本费![]() (元)与印刷册数
(元)与印刷册数![]() (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.


表中![]() .
.
为了预测印刷20千册时每册的成本费,建立了两个回归模型:![]() .
.
(1)根据散点图,拟认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求![]() 关于
关于![]() 的回归方程,并预测印刷20千册时每册的成本费.
的回归方程,并预测印刷20千册时每册的成本费.
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①用 刻画回归效果,当
刻画回归效果,当![]() 越大时,模型的拟合效果越差,反之则越好;②归纳推理是由特殊到一般的推理,而演绎推移则是由一般到特殊的推理;③综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”;④设有一个回归方程
越大时,模型的拟合效果越差,反之则越好;②归纳推理是由特殊到一般的推理,而演绎推移则是由一般到特殊的推理;③综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”;④设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位;⑤线性回归方程
平均增加5个单位;⑤线性回归方程![]() 必过点
必过点![]() .其中错误的个数有( )
.其中错误的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知4名学生和2名教师站在一排照相,求:
(1)中间二个位置排教师,有多少种排法?
(2)首尾不排教师,有多少种排法?
(3)两名教师不站在两端,且必须相邻,有多少种排法?
(4)两名教师不能相邻的排法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如下频率分布直方图:

(1)求直方图中![]() 的值;
的值;
(2)根据频率分布直方图估计样本数据的众数、中位数各是多少(结果保留整数);
(3)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,试计算数据落在
,试计算数据落在![]() 上的概率.
上的概率.
(参考数据:若![]() ,则
,则![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我市特色学校的发展状况,某调查机构得到如下统计数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(Ⅰ)根据上表数据,计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并说明
,并说明![]() 与
与![]() 的线性相关性强弱(已知:
的线性相关性强弱(已知:![]() ,则认为
,则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般;
线性相关性一般;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性较弱);
线性相关性较弱);
(Ⅱ)求![]() 关于
关于![]() 的线性回归方程,并预测我市2019年特色学校的个数(精确到个).
的线性回归方程,并预测我市2019年特色学校的个数(精确到个).
参考公式: 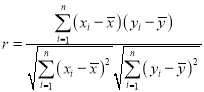 ,
,![]() ,
,![]() ,
,![]() ,
,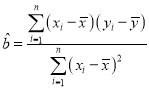 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com