
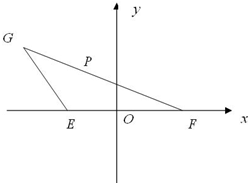
 已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,|
已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,|. |
| FG |
. |
| EF |
. |
| PE |
| 1 |
| 2 |
. |
| EG |
. |
| EG |
. |
| OE |
. |
| OA |
. |
| OB |
| PE |
| 1 |
| 2 |
| EG |
| PH |
| PH |
| EG |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 25 |
| y2 |
| 16 |
| OE |
| OA |
| OB |
| OA |
| OB |
| OB |
| 1 |
| 2 |
| OE |
| 72 | ||
16|m|+
|
| 25 |
| |m| |
| 9 |
| 5 |
| PE |
| 1 |
| 2 |
| EG |
| PH |
| PH |
| EG |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 25 |
| y2 |
| 16 |
| OE |
| OA |
| OB |
| OA |
| OB |
| OB |
| OE |
| OB |
| OA |
| OB |
| BE |
| BA |
|
| 96m |
| 16m2+25 |
| y1+y2 |
| 2 |
| 48m |
| 16m2+25 |
| 1 |
| 2 |
| OE |
| 1 |
| 2 |
| 48|m| |
| 16m2+25 |
| 72|m| |
| 16m2+25 |
| 72 | ||
16|m|+
|
| 25 |
| |m| |
| 5 |
| 4 |
| 25 |
| |m| |
| 9 |
| 5 |


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OM |
| ON |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
| OP |
| OM |
| ON |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年辽宁省沈阳市四校协作体高三(上)联考数学试卷(文科)(解析版) 题型:解答题
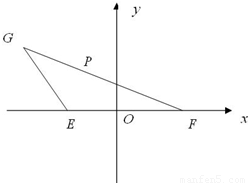 已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,
已知E、F是x轴上的点,坐标原点O为线段EF的中点,G、P是坐标平面上的动点,点P在线段FG上,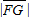 =10,
=10,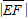 =6,
=6,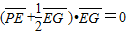
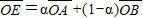 ,M为AB的中点,求△OEM面积的最大值.
,M为AB的中点,求△OEM面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com