
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人,这里的“六艺”其实源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”. 为弘扬中国传统文化,某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“数”必须排在前两节,“礼”和“乐”必须相邻安排的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由题意基本事件总数![]() ,其中“数”必须排在前两节,“礼”和“乐”必须相邻安排分“数”在第一节和第二节两类,“礼”和“乐”相邻用捆绑法即可求解.
,其中“数”必须排在前两节,“礼”和“乐”必须相邻安排分“数”在第一节和第二节两类,“礼”和“乐”相邻用捆绑法即可求解.
由题意知基本事件总数![]() ,
,
“数”必须排在前两节,“礼”和“乐”必须相邻可以分两类安排:
![]() “数”排在第一位,“礼”和“乐”两门课程相邻排课,则礼,乐相邻的位置有4个,考虑两者的顺序,有2种情况,
“数”排在第一位,“礼”和“乐”两门课程相邻排课,则礼,乐相邻的位置有4个,考虑两者的顺序,有2种情况,
剩下的3个全排列,安排在其他三个位置,有![]() 种情况,故有
种情况,故有![]() 种
种
![]() “数”排第二位, “礼”和“乐”两门课程相邻排课,则礼,乐相邻的位置有3个,考虑两者的顺序,有2种情况,剩下的3个全排列,安排在其他三个位置,有
“数”排第二位, “礼”和“乐”两门课程相邻排课,则礼,乐相邻的位置有3个,考虑两者的顺序,有2种情况,剩下的3个全排列,安排在其他三个位置,有![]() 种情况,
种情况,
则有![]() 种情况,
种情况,
由分类加法原理知满足“数”必须排在前两节,“礼”和“乐”必须相邻安排共有![]() 种情况,
种情况,
所以满足“数”必须排在前两节,“礼”和“乐”必须分开安排的概率为![]() .
.
故选:B


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中,AC=6,BA=BC=5,AD=CD=3![]() .
.
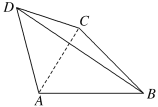
(1)求证:AC⊥BD;
(2)当四面体ABCD的体积最大时,求点A到平面BCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距和长半轴长都为2.过椭圆
的焦距和长半轴长都为2.过椭圆![]() 的右焦点
的右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 的左顶点,直线
的左顶点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,
,![]() .求证:以
.求证:以![]() 为直径的圆恒过点
为直径的圆恒过点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S-ABC中,侧棱SA,SB,SC两两成等角,且长度分别为a,b,c,设二面角S-BC-A,S-AC–B,S-AB-C的大小为![]() ,若
,若![]() 则α,β,γ的大小关系是( )
则α,β,γ的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行象棋比赛,采取五局三胜制(不考虑平局,先赢得三场的人为获胜者,比赛结束).根据前期的统计分析,得到甲在和乙的第一场比赛中,取胜的概率为0.5,受心理方面的影响,前一场比赛结果会对甲的下一场比赛产生影响,如果甲在某一场比赛中取胜,则下一场取胜率提高0.1,反之,降低0.1.则甲以3:1取得胜利的概率为( )
A.0.162B.0.18C.0.168D.0.174
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为非零实数,其前
的各项均为非零实数,其前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,
,![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对任意正整数
对任意正整数![]() 恒成立,若存在,求实数
恒成立,若存在,求实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,![]() ,_________,DC=2,在下面给出的三个条件中任选一个,补充在上面的问题中,并加以解答.(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)①
,_________,DC=2,在下面给出的三个条件中任选一个,补充在上面的问题中,并加以解答.(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)①![]() ;②
;②![]() ;③
;③![]() .
.
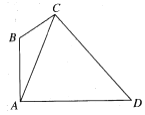
(1)求![]() 的大小;
的大小;
(2)求△ADC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com