
四面体ABCD中,AD与BC互相垂直,AD=2BC=4,且AB+BD=AC+CD=2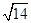 ,则四面体ABCD的体积的最大值是
,则四面体ABCD的体积的最大值是
A.4 B.2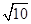 C.5 D.
C.5 D.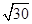
A
【解析】
试题分析:作BE⊥AD于E,连接CE,说明B与C都是在以AD为焦距的椭球上,且BE、CE都垂直于焦距AD,BE=CE.取BC中点F,推出四面体ABCD的体积的最大值,当△ABD是等腰直角三角形时几何体的体积最大,求解即可.解:
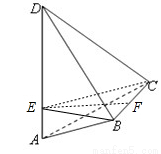
作BE⊥AD于E,连接CE,则AD⊥平面BEC,所以CE⊥AD,由题设,B与C都是在以AD为焦点的椭圆上,且BE、CE都垂直于焦距AD, AB+BD=AC+CD=2a,显然△ABD≌△ACD,所以BE=CE.取BC中点F,∴EF⊥BC,EF⊥AD,四面体ABCD的体积的最大值,只需EF最大即可,当△ABD是等腰直角三角形时几何体的体积最大,故可知答案为4,选A
考点:棱锥
点评:本题考查棱柱、棱锥、棱台的体积,考查空间想象能力,逻辑推理能力以及计算能力.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
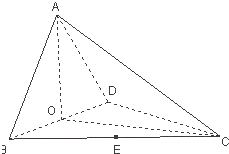 如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知O是△ABC内任意一点,连结AO,BO,CO并延长交对边于A′,B′,C′,则
已知O是△ABC内任意一点,连结AO,BO,CO并延长交对边于A′,B′,C′,则| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
| VO-BCD |
| VABCD |
| V0-ABD |
| VABCD |
| VO-ACD |
| VABCD |
| VO-ABC |
| VABCD |
| VO-BCD |
| VABCD |
| V0-ABD |
| VABCD |
| VO-ACD |
| VABCD |
| VO-ABC |
| VABCD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com