
已知函数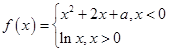 ,其中
,其中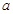 是实数,设
是实数,设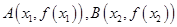 为该函数的图象上的两点,且
为该函数的图象上的两点,且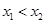 .
.
⑴指出函数 的单调区间;
的单调区间;
⑵若函数 的图象在点
的图象在点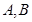 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求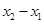 的最小值;
的最小值;
⑶若函数 的图象在点
的图象在点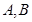 处的切线重合,求
处的切线重合,求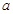 的取值范围.
的取值范围.
(1)单调减区间为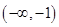 ,单调增区间为
,单调增区间为 ;(2)1;(3)
;(2)1;(3)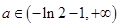 .
.
解析试题分析:(1)根据基本初等函数的性质知,分段函数 在
在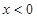 时是二次函数的一部分,有两个单调区间:增区间
时是二次函数的一部分,有两个单调区间:增区间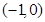 ,减区间
,减区间 ,
,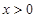 时是对数函数,只有一个单调增区间
时是对数函数,只有一个单调增区间 ;(2)对函数图象来讲,它在某点处的切线斜率等于该函数在此点处的导数,故有
;(2)对函数图象来讲,它在某点处的切线斜率等于该函数在此点处的导数,故有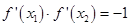 ,由于
,由于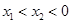 ,
,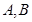 两点在
两点在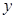 轴的左边,
轴的左边,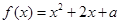 ,因此有
,因此有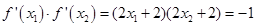 ,显然有
,显然有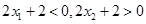 ,
,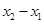 可以表示为关于
可以表示为关于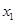 的函数,从而求出最小值(
的函数,从而求出最小值(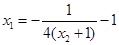 ,
,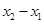
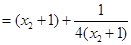 应用基本不等式即可得解)也可以直接凑配出基本不等式的形式,
应用基本不等式即可得解)也可以直接凑配出基本不等式的形式,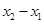 =
=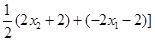 利用基本不等式);(3)这里我们首先分析
利用基本不等式);(3)这里我们首先分析 所处范围,结合图象易知
所处范围,结合图象易知 不可能在同一单调区间,只能是
不可能在同一单调区间,只能是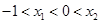 ,那么我们可得出
,那么我们可得出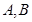 两点处的切线方程分别为
两点处的切线方程分别为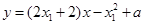 ,
,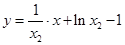 ,两条切线相同,则有
,两条切线相同,则有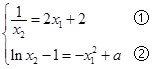 ,于是可把
,于是可把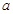 表示为
表示为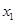 (或者
(或者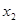 )的函数,把求
)的函数,把求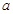 匠范围转化为求函数的值域.
匠范围转化为求函数的值域.
试题解析:(1)单调减区间为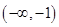 ,单调增区间为
,单调增区间为 4分
4分
(2)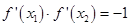 ,
,
当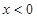 时,因为
时,因为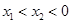 ,所以
,所以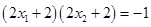 . 8分
. 8分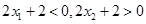
∴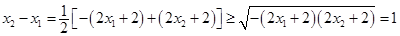
当且仅当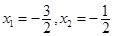 时等号成立,
时等号成立,
∴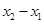 的最小值为1. 10分
的最小值为1. 10分
(3)当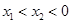 或
或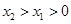 时,
时,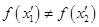 ,故
,故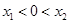
当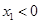 时,函数
时,函数 的图象在点
的图象在点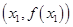 的切线方程为
的切线方程为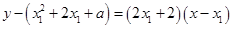
即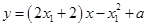
当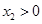 时,函数
时,函数 在
在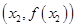 切线方程为
切线方程为
两切线重合的充要条件是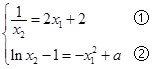 13分
13分
由①及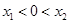 知
知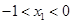
由①②得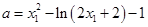
又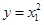 ,与
,与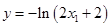 在
在 都为减函数.
都为减函数.
∴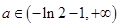 16分
16分
考点:(1)单调区间;(2)函数图象的切线及基本不等式;(3)切线与函数的值域.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
已知 是正数,
是正数, ,
, ,
, .
.
(Ⅰ)若 成等差数列,比较
成等差数列,比较 与
与 的大小;
的大小;
(Ⅱ)若 ,则
,则 三个数中,哪个数最大,请说明理由;
三个数中,哪个数最大,请说明理由;
(Ⅲ)若 ,
, ,
, (
( ),且
),且 ,
, ,
, 的整数部分分别是
的整数部分分别是

 求所有
求所有 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了在夏季降温和冬季供暖时减少能源消耗,房屋的屋顶和外墙需要建造隔热层,某栋建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度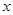 (单位:
(单位: )满足关系:
)满足关系:
若不建隔热层,每年能源消耗费用为8万元。设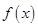 为隔热层建造费用与20年的能源消耗费用之和。
为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求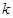 的值及
的值及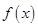 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用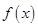 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品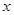 (百台),其总成本为
(百台),其总成本为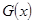 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入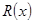 (万元)满足
(万元)满足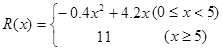 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
分别写出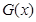 和利润函数
和利润函数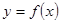 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本);
工厂生产多少台产品时,可使盈利最多?并求出此时每台产品的售价。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某医药研究所开发一种新药,据监测,如果成人按规定剂量服用该药,服药后每毫升血液中的含药量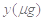 与服药后的时间
与服药后的时间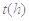 之间近似满足如图所示的曲线.其中
之间近似满足如图所示的曲线.其中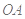 是线段,曲线段
是线段,曲线段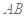 是函数
是函数
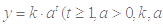 是常数
是常数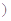 的图象.
的图象.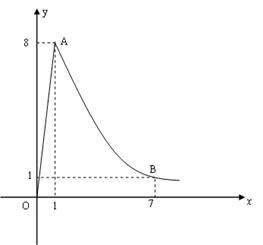
(1)写出服药后每毫升血液中含药量 关于时间
关于时间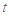 的函数关系式;
的函数关系式;
(2)据测定:每毫升血液中含药量不少于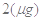 时治疗有效,假若某病人第一次服药为早上
时治疗有效,假若某病人第一次服药为早上 ,为保持疗效,第二次服药最迟是当天几点钟?
,为保持疗效,第二次服药最迟是当天几点钟?
(3)若按(2)中的最迟时间服用第二次药,则第二次服药后再过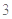
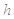 ,该病人每毫升血液中含药量为多少
,该病人每毫升血液中含药量为多少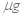 ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com