解:(I)∵f′(x)=x
2-2(a+1)x+4a(3分)
∴f′(3)=9-6(a+1)+4a=0得

(4分)
∵
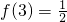
解得:b=-4(5分)
(II)∵f′(x)=x
2-2(a+1)x+4a=(x-2a)(x-2)
令f′(x)=0,即x=2a或x=2.(7分)
当a>1时,2a>2,∴f′(x)>0时,x>2a或x<2,即f(x)的单调递增区间为(-∞,2)和(2a,+∞).(8分)
当a=1时,f′(x)=(x-2)
2≥0,即f(x)的单调递增区间为(-∞,+∞).(9分)
当a<1时,2a<2,∴f′(x)>0时,x<2a或x>2,即f(x)的单调递增区间为(-∞,2a)和(2,+∞).(10分)
(Ⅲ)由题意可得:
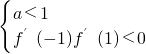
(12分)
∴(2a-1)(2a+1)<0
∴
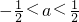
∴a的取值范围
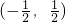
(14分)
分析:(I)先求导函数,利用函数f(x)在x=3处取得极小值是

,可得f′(3)=0,
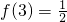
,从而可求a、b的值;
(II)先求导函数,f′(x)=x
2-2(a+1)x+4a=(x-2a)(x-2),比较2a与2的大小,从而进行分类讨论,进而可确定函数的单调递增区间
(Ⅲ)函数f(x)在(-1,1)上有且只有一个极值点,等价于f′(x)在(-1,1)上有且只有一个解;由(II)及零点存在定理可得
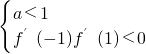
,从而可确定a的取值范围.
点评:本题以函数为载体,考查利用导数求函数的极值,考查利用导数确定函数的单调区间,理解函数极值的定义是解题的关键

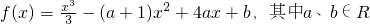
 ,求a、b的值;
,求a、b的值; (4分)
(4分)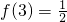 解得:b=-4(5分)
解得:b=-4(5分)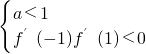 (12分)
(12分)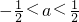
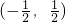 (14分)
(14分) ,可得f′(3)=0,
,可得f′(3)=0,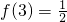 ,从而可求a、b的值;
,从而可求a、b的值;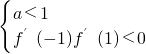 ,从而可确定a的取值范围.
,从而可确定a的取值范围.

 阅读快车系列答案
阅读快车系列答案