
(本题满分12分)已知函数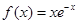 ,
,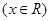 .
.
(1)求函数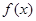 的单调区间和极值;
的单调区间和极值;
(2)已知函数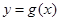 的图象与函数
的图象与函数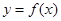 的图象关于直线
的图象关于直线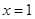 对称;
对称;
证明:当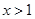 时,
时,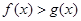
(3)如果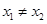 且
且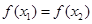 ,证明
,证明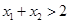
(Ⅰ) 在区间
在区间 内是增函数,在区间
内是增函数,在区间 内是减函数.
内是减函数.
函数 在
在 处取得极大值
处取得极大值 .且
.且 .
.
(Ⅱ)见解析;(Ⅲ)见解析。
【解析】本试题主要是考查了运用导数研究函数的性质的综合运用。
(1)利用导数,结合导数的符号与函数单调性的关系得到第一问中的单调区间和极值问题。
(2)先利用对称性求解函数的解析式,然后构造函数证明不等式恒成立,或者利用第一问的结论,结合对称性得到证明。
(3)由上可知函数的的单调性,结合性质可知不等式的证明。
(Ⅰ) .令
.令 ,则
,则 .
.
当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
增 |
极大值 |
减 |
所以 在区间
在区间 内是增函数,在区间
内是增函数,在区间 内是减函数.
内是减函数.
函数 在
在 处取得极大值
处取得极大值 .且
.且 .
.
(Ⅱ)因为函数 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,
对称,
所以 ,于是
,于是 .
.
记 ,则
,则 ,
, ,
,
当 时,
时, ,从而
,从而 ,又
,又 ,所以
,所以 ,
,
于是函数 在区间
在区间 上是增函数.
上是增函数.
因为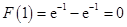 ,所以,当
,所以,当 时,
时, .因此
.因此 .
.
(Ⅲ)(1) 若 ,由(Ⅰ)及
,由(Ⅰ)及 ,得
,得 ,与
,与 矛盾;
矛盾;
(2) 若 ,由(Ⅰ)及
,由(Ⅰ)及 ,得
,得 ,与
,与 矛盾;
矛盾;
根据(1),(2)可得 .不妨设
.不妨设 .
.
由(Ⅱ)可知 ,所以
,所以 .
.
因为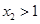 ,所以
,所以 ,又
,又 ,由(Ⅰ),
,由(Ⅰ), 在区间
在区间 内是增函数,
内是增函数,
所以  ,即
,即 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:安徽省合肥一中、六中、一六八中学2010-2011学年高二下学期期末联考数学(理 题型:解答题
(本题满分12分)已知△ 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 的大小;(2)若
的大小;(2)若 .求
.求 .
.
查看答案和解析>>
科目:高中数学 来源:2011届本溪县高二暑期补课阶段考试数学卷 题型:解答题
(本题满分12分)已知各项均为正数的数列 ,
, 的等比中项。
的等比中项。
(1)求证:数列 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省揭阳市高三调研检测数学理卷 题型:解答题
(本题满分12分)
已知椭圆 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点.
(1)若 ,且
,且 ,
, ,求
,求 、
、 的坐标;
的坐标;
(2)在(1)的条件下,过动点 作以
作以 为圆心、以1为半径的圆的切线
为圆心、以1为半径的圆的切线 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源:2010年辽宁省高二上学期10月月考理科数学卷 题型:解答题
(本题满分12分)已知椭圆 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量
(1)求椭圆的离心率
(2)设Q是椭圆上任意一点, 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com