解:(1)令x=y=1,f(2)=f(1)+f(1)+12+2k+3?k=0,则f(x+y)=f(x)+f(y)+3xy(x+y+2)+3
对于x,y∈R都成立
令x=t(t∈N*),y=1f(t+1)=f(t)+f(1)+3t(t+3)+3?f(t+1)-f(t)=3t
2+9t+4?f(2)-f(1)=3×1
2+9×1+4f(3)-f(2)=3×2
2+9×2+4
…f(t)=f(t-1)=3(t-1)
2+9×(t-1)+4
用叠加法 f(t)-f(1)=3[1
2+2
2+…+(t-1)
2]+9[1+2+…+(t-1)]+4+4•k…+4=
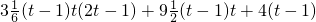
=t
3+3t
2-4
∴f(t)=t
3+3t
2-3(t≥2)又t=1适合上式f(t)=t
3+3t
2-3(t≥2)(t∈N*)
(2)若t∈N*,则t
3+3t
2-3=t?t
3-t+3(t
2+1)=0?(t-1)(t+1)(t+3)=0?t
1=1,t
2=-1,t
3=-3(舍)
又令x=y=0f(0)=-3
令y=-x-3=f(x)+f(-x)+(-6x
2)+3?f(x)+f(-x)=6x
2-6对x∈R都成立
若t为负整数,则f(t)=6t
2-6-f(-t)=6t
2-6+t
3-3t
2+3=t
3+3t
2-3
由t
3+3t
2-3=t(t+3)(t+1)(t-1)?t
1=-3,t
2=-1,t
3=1(舍)
若t=0,则f(t)═t无解 综上,满足f(t)=t,所有整数t为1,-1,-3;
(3)要使不等式恒成立,则只需

对t≥4,且t∈N*恒成立
即
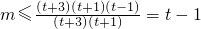
对t≥4,且t∈N*恒成立
即且m≤(t-1)
min=3
实数m最大值为3
分析:(1)令x=y=1,求得k=0,由于对于x,y∈R都成立,故令x=t(t∈N*),y=1,可得f(t+1)-f(t)=3t
2+9t+4,从而利用叠加法,可求f(t)的解析式;(2)对t进行分类讨论:若t∈N*,则t
3+3t
2-3=t?t
3-t+3(t
2+1)=0;若t为负整数,则f(t)=6t
2-6-f(-t)=6t
2-6+t
3-3t
2+3=t
3+3t
2-3;若t=0,则f(t)═t无解;(3)要使不等式恒成立,则只需

对t≥4,且t∈N*恒成立.
点评:本题考查抽象函数,赋值法是最常用的方法;不等式恒成立问题,通常利用最值法,本题属于中档题.

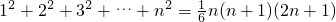 ;
;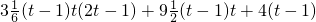 =t3+3t2-4
=t3+3t2-4 对t≥4,且t∈N*恒成立
对t≥4,且t∈N*恒成立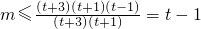 对t≥4,且t∈N*恒成立
对t≥4,且t∈N*恒成立 对t≥4,且t∈N*恒成立.
对t≥4,且t∈N*恒成立.
