
(本小题满分14分)
已知函数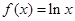 ,
,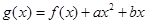 ,函数
,函数 的图象在点
的图象在点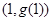 处的切线平行于
处的切线平行于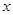 轴.
轴.
(1)确定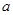 与
与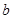 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意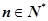 ,都有
,都有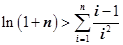 成立.
成立.
(1)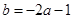
(2)当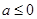 时,函数
时,函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在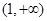 单调递减;
单调递减;
当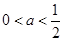 时,函数
时,函数 在
在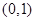 单调递增,在
单调递增,在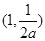 单调递减;在
单调递减;在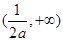 上单调递增;
上单调递增;
当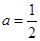 时,函数
时,函数 在
在 上单调递增,
上单调递增,
当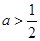 时,函数
时,函数 在
在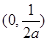 上单调递增,在
上单调递增,在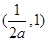 单调递减;在
单调递减;在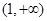 上单调递增.
上单调递增.
(3)可以利用放缩不等式证明也可以构造新数列利用数列的性质证明还可以构造函数利用导数证明
解析试题分析:(1)依题意得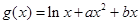 ,则
,则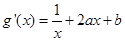
由函数 的图象在点
的图象在点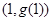 处的切线平行于
处的切线平行于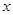 轴得:
轴得: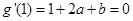
 ∴
∴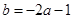 ……3分
……3分
(2)由(1)得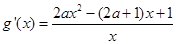
 ……4分
……4分
∵函数 的定义域为
的定义域为
∴当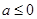 时,
时,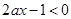 在
在 上恒成立,
上恒成立,
由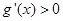 得
得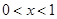 ,由
,由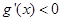 得
得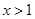 ,
,
即函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在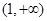 单调递减; ……5分
单调递减; ……5分
当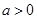 时,令
时,令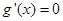 得
得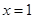 或
或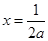 ,
,
若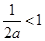 ,即
,即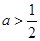 时,
时,
由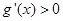 得
得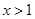 或
或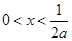 ,由
,由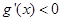 得
得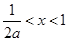 ,
,
即函数 在
在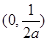 ,
,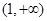 上单调递增,在
上单调递增,在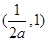 单调递减; ……6分
单调递减; ……6分
若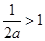 ,即
,即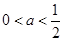 时,
时,
由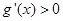 得
得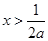 或
或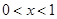 ,由
,由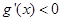 得
得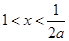 ,
,
即函数 在
在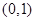 ,
,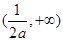 上单调递增,在
上单调递增,在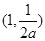 单调递减; ……7分
单调递减; ……7分
若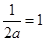 ,即
,即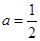 时,在
时,在 上恒有
上恒有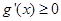 ,
,
即函数 在
在 上单调递增, ……8分
上单调递增, ……8分
综上得:当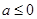 时,函数
时,函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在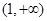 单调递减;
单调递减;
当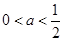 时,函数
时,函数 在
在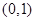 单调递增,在
单调递增,在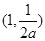 单调递减;在
单调递减;在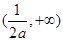 上单调递增;
上单调递增;
当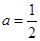 时,函数
时,函数 在
在

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分)生物体死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.
(Ⅰ)设生物体死亡时体内每克组织中的碳14的含量为1,根据上述规律,写出生物体内碳14的含量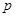 与死亡年数
与死亡年数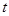 之间的函数关系式;
之间的函数关系式;
(Ⅱ)湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7℅,试推算马王堆汉墓的年代.(精确到个位;辅助数据: )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com