
如图,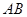 为圆
为圆 的直径,点
的直径,点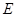 、
、 在圆
在圆 上,
上, ,矩形
,矩形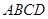 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
,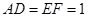 .
.

(1)求证: 平面
平面 ;
;
(2)设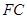 的中点为
的中点为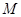 ,求证:
,求证: 平面
平面 ;
;
(3)设平面 将几何体
将几何体 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为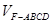 ,
, ,求
,求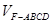
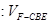 .
.
(1)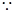 平面
平面 平面
平面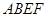 ,
,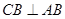 ,
, 平面
平面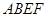
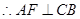 又
又 为圆
为圆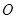 的直径,
的直径,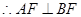
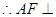 平面
平面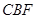 (2)设
(2)设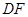 的中点为
的中点为 ,则
,则
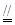
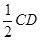 ,又
,又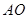
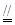
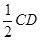 ,则
,则
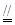
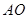 ,
,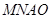 为平行四边形
为平行四边形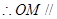
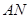 ,
,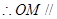 平面
平面 (3)
(3)
【解析】
试题分析:(1)证明:
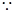 平面
平面 平面
平面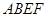 ,
,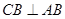 ,
,
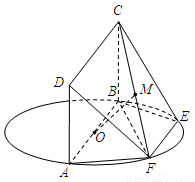
平面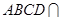 平面
平面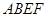 =
=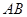 ,
, 平面
平面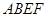 ,
,
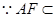 平面
平面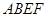 ,
,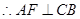 , 2分
, 2分
又 为圆
为圆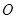 的直径,
的直径,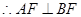 ,
,
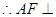 平面
平面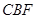 。 4分
。 4分
(2)设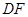 的中点为
的中点为 ,则
,则
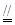
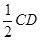 ,又
,又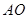
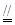
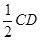 ,
,
则
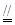
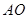 ,
,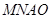 为平行四边形, 6分
为平行四边形, 6分
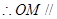
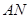 ,又
,又 平面
平面 ,
,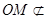 平面
平面 ,
,
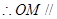 平面
平面 。 9分
。 9分
(3)过点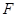 作
作 于
于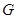 ,
,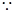 平面
平面 平面
平面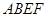 ,
,
 平面
平面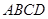 ,
,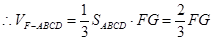 , 10分
, 10分
 平面
平面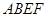 ,
,
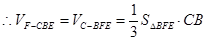
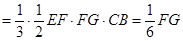 , 12分
, 12分
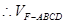
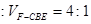 . 14分
. 14分
考点:线面垂直平行的判定及椎体的体积
点评:根据椎体的体积公式 ,求体积比主要是找到底面积和高的关系,判定线面垂直要判定直线垂直于平面内的两条相交直线,判定线面平行可转化为面外直线平行于面内直线或由两面平行得其中一面内直线平行于另外一面
,求体积比主要是找到底面积和高的关系,判定线面垂直要判定直线垂直于平面内的两条相交直线,判定线面平行可转化为面外直线平行于面内直线或由两面平行得其中一面内直线平行于另外一面


科目:高中数学 来源: 题型:
 如图,
如图,![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 、
、![]() 在圆
在圆![]() 上,且
上,且![]() ,矩形
,矩形![]() 所在的平面和圆
所在的平面和圆![]() 所在的平面互相垂直,且
所在的平面互相垂直,且![]() ,
,![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 的中点为
的中点为![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(Ⅲ)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2010年湖南省六校高三第二次联考数学(文)试题 题型:解答题
(本小题满分12分)如图, 为圆
为圆 的直径,点
的直径,点 、
、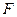 在圆
在圆 上,
上,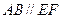 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
, .
.
(1) 求证:
求证: 平面
平面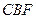 ;
;
(2)设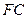 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;
(3)设平面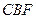 将几何体
将几何体 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为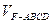 ,
,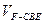 ,求
,求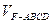
 .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西省高三第四次模拟考试文科数学试卷(解析版) 题型:解答题
如图, 为圆
为圆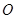 的直径,点
的直径,点 、
、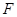 在圆
在圆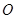 上,矩形
上,矩形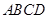 所在的平面和圆
所在的平面和圆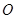 所在的平面互相垂直,且
所在的平面互相垂直,且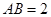 ,
,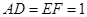 .
.

(Ⅰ)求证: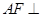 平面
平面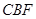 ;
;
(Ⅱ)求三棱锥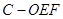 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省泉州四校高三第二次联考考试文科数学 题型:解答题
.(本题满分12分)如图,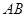 为圆
为圆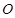 的直径,点
的直径,点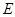 、
、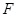 在圆
在圆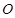 上,
上,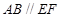 ,矩形
,矩形 的边
的边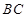 垂直于圆
垂直于圆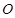 所在的平面,且
所在的平面,且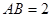 ,
,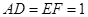 .
.
(1)求证: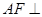 平面
平面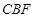 ;
;
(2)设 的中点为
的中点为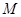 ,求证:
,求证: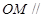 平面
平面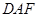 ;
;
(3)求三棱锥的体积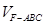 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省姜堰市二中学高三学情调查数学试卷 题型:解答题
(本小题满分14分)
如图,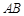 为圆
为圆 的直径,点
的直径,点 、
、 在圆
在圆 上,且
上,且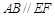 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)设 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;
(3)设平面 将几何体
将几何体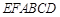 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为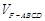 ,
, ,
,
求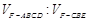
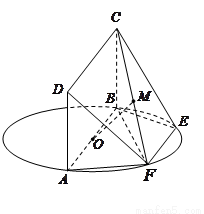
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com