
【题目】设函数![]() .
.
(![]() )若
)若![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
(![]() )若函数
)若函数![]() 在区间
在区间![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围.
的取值范围.
(![]() )过坐标原点
)过坐标原点![]() 作曲线
作曲线![]() 的切线,证明:切点的横坐标为
的切线,证明:切点的横坐标为![]() .
.
【答案】(![]() )单调减区间为
)单调减区间为![]() ,单调增区间为
,单调增区间为![]() .(
.(![]() )
)![]() (
(![]() )见解析
)见解析
【解析】试题分析:(1)当![]() 时,求出函数的导函数
时,求出函数的导函数![]() ,分别令
,分别令![]() 和
和![]() ,解出不等式得单调区间;(2)函数
,解出不等式得单调区间;(2)函数![]() 在区间
在区间![]() 上是减函数,即
上是减函数,即![]() 对任意
对任意![]() 恒成立,利用分离参数法可得最后结果;(3)设切点为
恒成立,利用分离参数法可得最后结果;(3)设切点为![]() ,对函数进行求导,根据导数的几何意义得
,对函数进行求导,根据导数的几何意义得![]() ,根据切线过原点,可得斜率为
,根据切线过原点,可得斜率为![]() ,两者相等化简可得
,两者相等化简可得![]() ,先证存在性,再通过单调性证明唯一性.
,先证存在性,再通过单调性证明唯一性.
试题解析:(![]() )当
)当![]() 时,
时, ![]() ,
, ![]() ,令
,令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,∴函数
,∴函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .
.
(![]() )
)![]() ,∵
,∵![]() 在区间
在区间![]() 上是减函数,∴
上是减函数,∴![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,易知
,易知![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,∴
,∴![]() .
.
(![]() )设切点为
)设切点为![]() ,
, ![]() ,∴切线的斜率
,∴切线的斜率![]() ,
,
又切线过原点, ![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ,存在性,
,存在性, ![]() 满足方程
满足方程![]() ,
,
所以![]() 是方程
是方程![]() 的根唯一性,
的根唯一性,
设![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,∴方程
,∴方程![]() 有唯一解
有唯一解![]() ,综上,过坐标原点
,综上,过坐标原点![]() 作曲线
作曲线![]() 的切线,则切点的横坐标为
的切线,则切点的横坐标为![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池ABCD及其矩形附属设施EFGH,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为O,半径为R,矩形的一边AB在直径上,点C、D、G、H在圆周上,E、F在边CD上,且![]() ,设
,设![]()
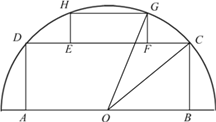
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)当![]() 为何值时,能符合园林局的要求?
为何值时,能符合园林局的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,其图象上存在一点
,其图象上存在一点![]() ,使此处切线的斜率
,使此处切线的斜率![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,方程
时,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在曲线
在曲线![]() 上,⊙
上,⊙![]() 过原点
过原点![]() ,且与
,且与![]() 轴的另一个交点为
轴的另一个交点为![]() ,若线段
,若线段![]() ,⊙
,⊙![]() 和曲线
和曲线![]() 上分别存在点
上分别存在点![]() 、点
、点![]() 和点
和点![]() ,使得四边形
,使得四边形![]() (点
(点![]() ,
, ![]() ,
, ![]() ,
, ![]() 顺时针排列)是正方形,则称点
顺时针排列)是正方形,则称点![]() 为曲线
为曲线![]() 的“完美点”.那么下列结论中正确的是( ).
的“完美点”.那么下列结论中正确的是( ).
A. 曲线![]() 上不存在”完美点”
上不存在”完美点”
B. 曲线![]() 上只存在一个“完美点”,其横坐标大于
上只存在一个“完美点”,其横坐标大于![]()
C. 曲线![]() 上只存在一个“完美点”,其横坐标大于
上只存在一个“完美点”,其横坐标大于![]() 且小于
且小于![]()
D. 曲线![]() 上存在两个“完美点”,其横坐标均大于
上存在两个“完美点”,其横坐标均大于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型娱乐场有两种型号的水上摩托,管理人员为了了解水上摩托的使用及给娱乐城带来的经济收入情况,对该场所最近6年水上摩托的使用情况进行了统计,得到相关数据如表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
使用率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)请根据以上数据,用最小二乘法求水上摩托使用率![]() 关于年份代码
关于年份代码![]() 的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
(2)随着生活水平的提高,外出旅游的老百姓越来越多,该娱乐场根据自身的发展需要,准备重新购进一批水上摩托,其型号主要是目前使用的Ⅰ型、Ⅱ型两种,每辆价格分别为1万元、1.2万元.根据以往经验,每辆水上摩托的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:
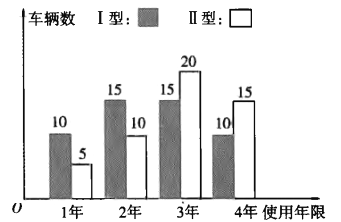
已知每辆水上摩托从购入到淘汰平均年收益是0.8万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润![]() 收益
收益![]() 购车成本)的期望值为参考值,则该娱乐场的负责人应该选购Ⅰ型水上摩托还是Ⅱ型水上摩托?
购车成本)的期望值为参考值,则该娱乐场的负责人应该选购Ⅰ型水上摩托还是Ⅱ型水上摩托?
附:回归直线方程为![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程选讲
在直角坐标系![]() 中,曲线C1的参数方程为
中,曲线C1的参数方程为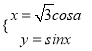 (a为参数),以原点O为极点,
(a为参数),以原点O为极点,
以x轴正半轴为极轴,建立极坐标系,曲 线C2的极坐标方程为![]()
(1)求曲线C1的普通方程与曲线C2的直角坐标方程.
(2)设P为曲线C1上的动点,求点P到C2上点的距离的最小值,并求此时点P坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定一个数列{an},在这个数列里,任取m(m≥3,m∈N*)项,并且不改变它们在数列{an}中的先后次序,得到的数列称为数列{an}的一个m阶子数列.已知数列{an}的通项公式为an=![]() (n∈N*,a为常数),等差数列a2,a3,a6是数列{an}的一个3阶子数列.
(n∈N*,a为常数),等差数列a2,a3,a6是数列{an}的一个3阶子数列.
(1)求a的值;
(2)等差数列b1,b2,…,bm是{an}的一个m (m≥3,m∈N*) 阶子数列,且b1=![]() (k为常数,k∈N*,k≥2),求证:m≤k+1;
(k为常数,k∈N*,k≥2),求证:m≤k+1;
(3)等比数列c1,c2,…,cm是{an}的一个m (m≥3,m∈N*) 阶子数列,
求证:c1+c2+…+cm≤2-![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com