
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=AA1=2,AC= ![]() ,过BC的中点D作平面ACB1的垂线,交平面ACC1A1于E,则BE与平面ABB1A1所成角的正切值为( )
,过BC的中点D作平面ACB1的垂线,交平面ACC1A1于E,则BE与平面ABB1A1所成角的正切值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:连结A1C,A1B,取A1C的中点E,连结DE,BE, ∵AC⊥AB,AC⊥AA1 , ∴AC⊥平面AA1B1B,∴AC⊥A1B.
∵AB=AA1 , ∴四边形AA1B1B是正方形,∴A1B⊥B1A,
∴A1B⊥平面B1CD,
∵D为BC的中点,E为A1C的中点,∴DE∥A1B,
∴DE⊥平面B1CD.
取A1A的中点F,连结EF,BF,则EF⊥平面AA1B1B,
∴∠EBF为BE与平面ABB1A1所成角.
∵EF= ![]() =
= ![]() ,AF=
,AF= ![]() =1,AB=2,
=1,AB=2,
∴BF= ![]() ,∴tan∠EBF=
,∴tan∠EBF= ![]() =
= ![]() .
.
故选C.
【考点精析】认真审题,首先需要了解空间角的异面直线所成的角(已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 ).
).


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且满足S4=24,S7=63. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2sinxcosx+3cos2x. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若x∈[0, ![]() ],求函数f(x)的最值及相应x的取值.
],求函数f(x)的最值及相应x的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于序列A0:a0 , a1 , a2 , …,an(n∈N*),实施变换T得序列A1:a1+a2 , a2+a3 , …,an﹣1+an , 记作A1=T(A0):对A1继续实施变换T得序列A2=T(A1)=T(T(A0)),记作A2=T2(A0);…;An﹣1=Tn﹣1(A0).最后得到的序列An﹣1只有一个数,记作S(A0). (Ⅰ)若序列A0为1,2,3,求S(A0);
(Ⅱ)若序列A0为1,2,…,n,求S(A0);
(Ⅲ)若序列A和B完全一样,则称序列A与B相等,记作A=B,若序列B为序列A0:1,2,…,n的一个排列,请问:B=A0是S(B)=S(A0)的什么条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.得到甲、乙两位学生成绩的茎叶图.
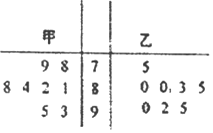
(1)现要从中选派一人参加数学竞赛,对预赛成绩的平均值和方差进行分析,你认为哪位学生的成绩更稳定?请说明理由;
(2)求在甲同学的8次预赛成绩中,从不小于80分的成绩中随机抽取2个成绩,列出所有结果,并求抽出的2个成绩均大于85分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x+2|+|x﹣a|,x∈R
(1)若a<0,且log2f(x)>2对任意x∈R恒成立,求实数a的取值范围;
(2)若a>0,且关于x的不等式f(x)< ![]() x有解,求实数a的取值范围.
x有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项中,奇数项的和为56,偶数项的和为48,且
项中,奇数项的和为56,偶数项的和为48,且![]() (其中
(其中![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,…,
,…,![]() ,…是一个等比数列,其中
,…是一个等比数列,其中![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)若存在实数![]() ,
,![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域为R的偶函数y=f(x)满足f(x+2)=﹣f(x),且当x∈[0,2]时,f(x)=2﹣x2 , 则方程f(x)=sin|x|在[﹣3π,3π]内根的个数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断错误的是
A. 若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ;
;
B. 若![]() 组数据
组数据![]() 的散点都在
的散点都在![]() 上,则相关系数
上,则相关系数![]() ;
;
C. 若随机变量![]() 服从二项分布:
服从二项分布: ![]() , 则
, 则![]() ;
;
D. ![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com