
已知函数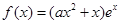 ,其中e是自然数的底数,
,其中e是自然数的底数,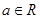 .
.
(1)当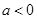 时,解不等式
时,解不等式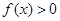 ;
;
(2)当 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程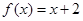 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若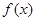 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求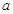 的取值范围.
的取值范围.
⑴因为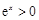 ,所以不等式
,所以不等式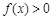 即为
即为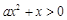 ,
,
又因为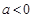 ,所以不等式可化为
,所以不等式可化为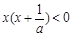 ,
,
所以不等式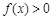 的解集为
的解集为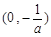 .………………………………………4分
.………………………………………4分
⑵当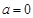 时, 方程即为
时, 方程即为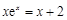 ,由于
,由于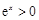 ,所以
,所以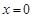 不是方程的解,
不是方程的解,
所以原方程等价于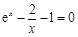 ,令
,令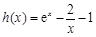 ,
,
因为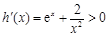 对于
对于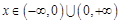 恒成立,
恒成立,
所以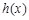 在
在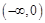 和
和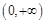 内是单调增函数,……………………………6分
内是单调增函数,……………………………6分
又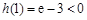 ,
,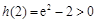 ,
,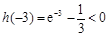 ,
,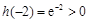 ,
,
所以方程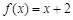 有且只有两个实数根,且分别在区间
有且只有两个实数根,且分别在区间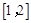 和
和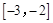 上,
上,
所以整数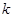 的所有值为
的所有值为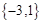 .……………………………………………8分
.……………………………………………8分
⑶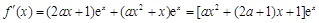 ,
,
①当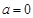 时,
时,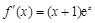 ,
,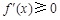 在
在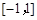 上恒成立,当且仅当
上恒成立,当且仅当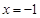 时
时
取等号,故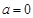 符合要求;………………………………………………………10分
符合要求;………………………………………………………10分
②当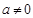 时,令
时,令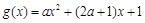 ,因为
,因为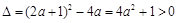 ,
,
所以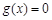 有两个不相等的实数根
有两个不相等的实数根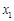 ,
,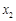 ,不妨设
,不妨设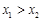 ,
,
因此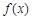 有极大值又有极小值.
有极大值又有极小值.
若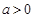 ,因为
,因为 ,所以
,所以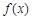 在
在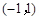 内有极值点,
内有极值点,
故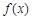 在
在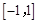 上不单调.………………………………………………………12分
上不单调.………………………………………………………12分
若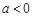 ,可知
,可知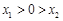 ,
,
因为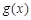 的图象开口向下,要使
的图象开口向下,要使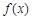 在
在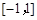 上单调,因为
上单调,因为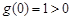 ,
,
必须满足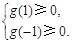 即
即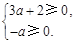 所以
所以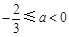 .--------------------------14分
.--------------------------14分
综上可知,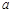 的取值范围是
的取值范围是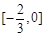 .………………………………………16分
.………………………………………16分
【解析】略


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012-2013学年江西省、南昌十中高三第四次联考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)
已知函数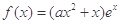 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.
(1)当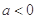 时,解不等式
时,解不等式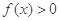 ;
;
(2)当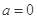 时,求正整数k的值,使方程
时,求正整数k的值,使方程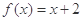 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若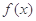 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求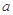 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届江苏省无锡市高一下期中数学(艺术)试卷(解析版) 题型:解答题
(本题16分)已知函数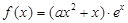 ,其中e是自然数的底数,
,其中e是自然数的底数,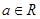 ,
,
(1)当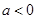 时,解不等式
时,解不等式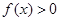 ;
;
(2)若当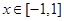 时,不等式
时,不等式 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)当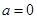 时,试判断:是否存在整数k,使得方程
时,试判断:是否存在整数k,使得方程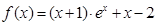 在
在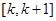
上有解?若存在,请写出所有可能的k的值;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省苏北四市(徐、连、淮、宿)高三元月调研测试数学试卷 题型:解答题
(本小题满分16分)已知函数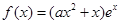 ,其中e是自然数的底数,
,其中e是自然数的底数,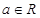 。
。
(1)当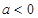 时,解不等式
时,解不等式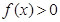 ;
;
(2)若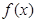 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求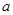 的取值范围;
的取值范围;
(3)当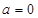 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程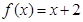 在[k,k+1]上有解。
在[k,k+1]上有解。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() ,其中e是自然数的底数,
,其中e是自然数的底数,![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)当![]() 时,求正整数k的值,使方程
时,求正整数k的值,使方程![]() 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若![]() 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com