练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数.

    （Ⅰ）若x＝时，取得极值，求的值；

    （Ⅱ）若在其定义域内为增函数，求的取值范围；

    （Ⅲ）设，当=－1时，证明在其定义域内恒成立，并证明（）.

    （Ⅰ）（Ⅱ）的取值范围是（Ⅲ）见解析


    解析:

    ，

    （Ⅰ）因为时，取得极值，所以，

     即    故．     ………………………………………………3分

    （Ⅱ）的定义域为.

    方程的判别式,

    (1) 当, 即时，,

    在内恒成立, 此时为增函数.

    (2) 当, 即或时，

    要使在定义域内为增函数,

    只需在内有即可,

    设，

    由   得 ,    所以.

    由(1) (2)可知,若在其定义域内为增函数，的取值范围是.

    ………………………………………………9分

    （Ⅲ）证明：，当=－1时，，其定义域是，

    令，得.则在处取得极大值，也是最大值.

    而.所以在上恒成立.因此.

    因为，所以.则.

    所以

    =

    <

    ==.

    所以结论成立.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•江苏三模）已知函数f（x）=x2+2ax+1（a∈R），f′（x）是f（x）的导函数．
    （1）若x∈[-2，-1]，不等式f（x）≤f′（x）恒成立，求a的取值范围；
    （2）解关于x的方程f（x）=|f′（x）|；
    （3）设函数g(x)=
    f′(x)，f(x)≥f′(x)
    f(x)，f(x)＜f′(x)
    ，求g（x）在x∈[2，4]时的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f(x)=log
    1
    2
    x+1
    x-1
    ．
    （1）判断函数f（x）的奇偶性，并证明；
    （2）证明函数f（x）在（1，+∞）上是增函数；
    （3）若x∈[3，+∞）时，不等式f(x)＞(
    1
    2
    )x+m    恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数y=1-
    2x+1-n
    x2+x+1
    （n∈N*）的最小值为an，最大值为bn，又Cn=3（an+bn）-9
    （1）求数列{an}的通项公式；
    （2）求
    lim
    n→∞
    		C1+C2+…+Cn
    Cn
    （n∈N*）的值
    （3）设Sn=
    1
    C1
    +
    1
    C2
    +…+
    1
    Cn
    ，dn=S2n+1-Sn    ，是否存在最小的整数m，使对任意的n∈N*都有dn＜
    m
    25
    成立？若存在，求出m的值；若不存在请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年西工大附中文）设函数，其中

    （Ⅰ）若f(x)在x=3处取得极值，求常数a 的值；

    （Ⅱ）若f(x)在上为增函数，求a的取值范围

    查看答案和解析>>

    科目：高中数学 来源：2012年河南省普通高中毕业班高考适应性测试数学试卷（理科）（解析版） 题型：解答题

    设函数．
    （1）若x=1是f（x）的极大值点，求a的取值范围．
    （2）当a=0，b=-1时，函数F（x）=f（x）-λx2有唯一零点，求正数λ的值．

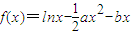    查看答案和解析>>

    同步练习册答案