练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设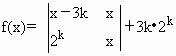(x∈R，k为正整数)

    (1)分别求出当k＝1，k＝2时方程f(x)＝0的解

    (2)设f(x)≤0的解集为[a2k－1，a2k]，求a1＋a2＋a3＋a4的值及数列{an}的前2n项和

    (3)对于(2)中的数列{an}，设，求数列{bn}的前n项和Tn的最大值．

    答案：
    解析：

    　　解：(1)

    　　当K＝1时，所以方程的解为　2分

    　　当K＝2时，所以方程的解为　4分

    　　(2)由即的解集为．

    　　∴，5分

    　　∴，．

    　　∴　7分

    　　

    　　　8分

    　　．9分

    　　　10分

    　　(3)

    　　

    　　　11分

    　　时，．12分

    　　n为奇数时，，即，13分

    　　n为偶数时，，即，14分

    　　∴Tn的最大值必为Tn的偶数项　15分

    　　故当n为偶数时时，

    　　

    　　．16分

    　　∴n为偶数时，在nÎ N*上为递减数列．17分

    　　

    　　∴．18分

    　　解法2：　11分

    　　

    　　＝　12分

    　　当n是偶数时　13分

    　　当n是奇数时　14分

    　　(1)当n是偶数时

    　　由于＝　15分

    　　所以{Tn}单调递减，所以　16分

    　　(2)当n是奇数

    　　＝

    　　{Tn}单调递增　17分

    　　所以此时Tn无最大值　18分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    规定Cmx=
    x(x-1)…(x-m+1)
    m！
    ，其中x∈R，m是正整数，且C0x=1，这是组合数Cmn（n、m是正整数，且m≤n）的一种推广．
    （1）求C3-15的值；
    （2）设x＞0，当x为何值时，
    C
    3
    x
    (C
    1
    x
    )2
    取得最小值？
    （3）组合数的两个性质；
    ①Cmn=Cn-mm． ②Cmn+Cm-1n=Cmn+1．
    是否都能推广到Cmx（x∈R，m是正整数）的情形？若能推广，则写出推广的形式并给出证明；若不能，则说明理由．
    变式：规定Axm=x（x-1）…（x-m+1），其中x∈R，m为正整数，且Ax0=1，这是排列数Anm（n，m是正整数，且m≤n）的一种推广．
    （1）求A-153的值；
    （2）排列数的两个性质：①Anm=nAn-1m-1，②Anm+mAnm-1=An+1m．（其中m，n是正整数）是否都能推广到Axm（x∈R，m是正整数）的情形？若能推广，写出推广的形式并给予证明；若不能，则说明理由；
    （3）确定函数Ax3的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义：
    .
    a    b
    c    d 
    .
    =ad-bc    ，设f(x)=  
    .
    x-3k    x
    2k          x 
    .
    +3k•2k    （x∈R，k为正整数）
    （1）分别求出当k=1，k=2时方程f（x）=0的解
    （2）设f（x）≤0的解集为[a2k-1，a2k]，求a1+a2+a3+a4的值及数列{an}的前2n项和
    （3）对于（2）中的数列{an}，设bn=
    (-1)n
    a2n-1a2n
    ，求数列{bn}的前n项和Tn的最大值．

    查看答案和解析>>

    科目：高中数学 来源：2010年广东省深圳市罗湖区高考数学精编模拟试卷（文科）（解析版） 题型：解答题

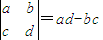    定义：，设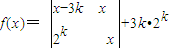（x∈R，k为正整数）
    （1）分别求出当k=1，k=2时方程f（x）=0的解
    （2）设f（x）≤0的解集为[a2k-1，a2k]，求a1+a2+a3+a4的值及数列{an}的前2n项和
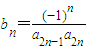    （3）对于（2）中的数列{an}，设，求数列{bn}的前n项和Tn的最大值．

    查看答案和解析>>

    科目：高中数学 来源：2011年云南省高三数学一轮复习章节练习：计数原理（解析版） 题型：解答题

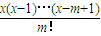    规定Cmx=，其中x∈R，m是正整数，且Cx=1，这是组合数Cmn（n、m是正整数，且m≤n）的一种推广．
    （1）求C3-15的值；
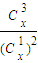    （2）设x＞0，当x为何值时，取得最小值？
    （3）组合数的两个性质；
    ①Cmn=Cn-mm． ②Cmn+Cm-1n=Cmn+1．
    是否都能推广到Cmx（x∈R，m是正整数）的情形？若能推广，则写出推广的形式并给出证明；若不能，则说明理由．
    变式：规定Axm=x（x-1）…（x-m+1），其中x∈R，m为正整数，且Ax=1，这是排列数Anm（n，m是正整数，且m≤n）的一种推广．
    （1）求A-153的值；
    （2）排列数的两个性质：①Anm=nAn-1m-1，②Anm+mAnm-1=An+1m．（其中m，n是正整数）是否都能推广到Axm（x∈R，m是正整数）的情形？若能推广，写出推广的形式并给予证明；若不能，则说明理由；
    （3）确定函数Ax3的单调区间．

    查看答案和解析>>

    同步练习册答案