
【题目】已知椭圆:![]() 的右焦点为
的右焦点为![]() 点的坐标为
点的坐标为![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)经过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,求
两点,求![]() 面积的最大值;
面积的最大值;
(3)是否存在直线![]() 交椭圆于
交椭圆于![]() 两点,使点
两点,使点![]() 为
为![]() 的垂心(垂心:三角形三边高线的交点)?若存在,求出直线
的垂心(垂心:三角形三边高线的交点)?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由![]() 是等腰直角三角形,可得
是等腰直角三角形,可得![]() ,从而可得椭圆方程;
,从而可得椭圆方程;
(2)设过点![]() 的直线
的直线![]() 的方程为
的方程为![]() ,
,![]() 的横坐标分别为
的横坐标分别为![]() ,求出
,求出![]() 的最大值,即可求得
的最大值,即可求得![]() 面积
面积![]() 的最大值;
的最大值;
(3)假设存在直线![]() 交椭圆于
交椭圆于![]() 两点,且使点
两点,且使点![]() 为
为![]() 的垂心,设直线
的垂心,设直线![]() 的方程为
的方程为![]() ,代入椭圆方程,利用韦达定理结合
,代入椭圆方程,利用韦达定理结合![]() ,即可求得结论.
,即可求得结论.
解:(1)由![]() 是等腰直角三角形,可得
是等腰直角三角形,可得![]() ,
,
故椭圆方程为![]() ;
;
(2)设过点![]() 的直线
的直线![]() 的方程为
的方程为![]() ,
,![]() 的横坐标分别为
的横坐标分别为![]() ,
,
将线![]() 的方程为
的方程为![]() 代入椭圆方程,
代入椭圆方程,
消元可得![]() ,
,
∴![]() ,
,
![]() ,
,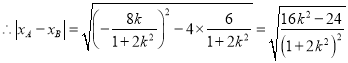 ,
,
令![]() ,则
,则![]()
令![]() ,则
,则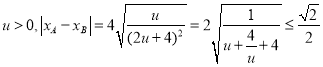 (当且仅当
(当且仅当![]() 时取等号)
时取等号)
又![]() 面积
面积![]() ,
,
∴△AOB面积的最大值为![]() ;
;
(3)假设存在直线![]() 交椭圆于
交椭圆于![]() 两点,且使点
两点,且使点![]() 为
为![]() 的垂心,
的垂心,
设![]() ,
,
因为![]() ,所以
,所以![]() .
.
于是设直线![]() 的方程为
的方程为![]() ,代入椭圆方程,
,代入椭圆方程,
消元可得![]() .
.
由![]() ,得
,得![]() ,且
,且![]() ,
,
由题意应有![]() ,所以
,所以![]() ,
,
所以![]() .
.
整理得![]() .
.
解得![]() 或
或![]() .
.
经检验,当![]() 时,
时,![]() 不存在,故舍去.
不存在,故舍去.
∴当![]() 时,所求直线
时,所求直线![]() 存在,且直线l的方程
存在,且直线l的方程![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C:![]() 上,该椭圆的左顶点A到直线
上,该椭圆的左顶点A到直线![]() 的距离为
的距离为![]() .
.
![]() 求椭圆C的标准方程;
求椭圆C的标准方程;
![]() 若线段MN平行于y轴,满足
若线段MN平行于y轴,满足![]() ,动点P在直线
,动点P在直线![]() 上,满足
上,满足![]() 证明:过点N且垂直于OP的直线过椭圆C的右焦点F.
证明:过点N且垂直于OP的直线过椭圆C的右焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() .过
.过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 位于第一象限,且
位于第一象限,且![]() ,求
,求![]() 的外接圆的方程.
的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某大学中随机选取7名女大学生,其身高x(单位:cm)和体重y(单位:kg)数据如下表:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
身高x | 163 | 164 | 165 | 166 | 167 | 168 | 169 |
体重y | 52 | 52 | 53 | 55 | 54 | 56 | 56 |
(1)求y关于x的回归方程;
(2)利用(1)中的回归方程,分析这7名女大学生的身高和体重的变化,并预报一名身高为172cm的女大学生的体重.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了庆祝第一个农民丰收节,西部山区某村统计了自2011年以来每年的年总收入,其中2018年统计的是1月到8月的总收入,统计结果如图所示.根据图形,下列四个判断中,错误的是( )
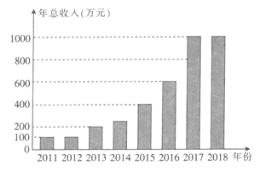
A.从2012年起,年总收入逐年增加B.2017年的年总收入在2016年的基础上翻了番
C.年份数与年总收入成正相关D.由图可预测从2014年起年总收入增长加快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正![]() 所在平面垂直平面
所在平面垂直平面![]() ,且边
,且边![]() 在平面
在平面![]() 内,过
内,过![]() 、
、![]() 分别作两个平面
分别作两个平面![]() 、
、![]() (与正
(与正![]() 所在平面不重合),则以下结论错误的是( )
所在平面不重合),则以下结论错误的是( )
A.存在平面![]() 与平面
与平面![]() ,使得它们的交线
,使得它们的交线![]() 和直线
和直线![]() 所成角为
所成角为![]()
B.直线![]() 与平面
与平面![]() 所成的角不大于
所成的角不大于![]()
C.平面![]() 与平面
与平面![]() 所成锐二面角不小于
所成锐二面角不小于![]()
D.平面![]() 与平面
与平面![]() 所成锐二面角不小于
所成锐二面角不小于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,焦点为
,焦点为![]() ,直线
,直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,
两点,![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作
作![]() 轴的垂线交抛物线
轴的垂线交抛物线![]() 于点
于点![]() .
.
(1)求抛物线![]() 的焦点坐标;
的焦点坐标;
(2)若抛物线![]() 上有一点
上有一点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() ,求此时
,求此时![]() 的值;
的值;
(3)是否存在实数![]() ,使
,使![]() 是以
是以![]() 为直角顶点的直角三角形?若存在,求出
为直角顶点的直角三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从4名男同学中选出2人,6名女同学中选出3人,并将选出的5人排成一排.
(1)共有多少种不同的排法?
(2)若选出的2名男同学不相邻,共有多少种不同的排法?(用数字表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com