
【题目】椭圆![]() 与
与![]() 的中心在原点,焦点分别在
的中心在原点,焦点分别在![]() 轴与
轴与![]() 轴上,它们有相同的离心率
轴上,它们有相同的离心率![]() ,并且
,并且![]() 的短轴为
的短轴为![]() 的长轴,
的长轴,![]() 与
与![]() 的四个焦点构成的四边形面积是
的四个焦点构成的四边形面积是![]() .
.
(1)求椭圆![]() 与
与![]() 的方程;
的方程;
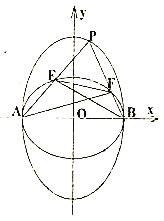
(2)设![]() 是椭圆
是椭圆![]() 上非顶点的动点,
上非顶点的动点,![]() 与椭圆
与椭圆![]() 长轴两个顶点
长轴两个顶点![]() ,
,![]() 的连线
的连线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
,![]() 点.
点.
(i)求证:直线![]() ,
,![]() 斜率之积为常数;
斜率之积为常数;
(ii)直线![]() 与直线
与直线![]() 的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
【答案】(1)![]() ,
,![]() .(2)(i) 见解析(ii)
.(2)(i) 见解析(ii)![]() .
.
【解析】试题分析:(1)椭圆离心率![]() ,又
,又![]() ,所以
,所以![]() ,设
,设![]() ,则根据题中条件可设
,则根据题中条件可设![]() ,于是根据椭圆的对称性可知,四个焦点构成的四边形为菱形,面积
,于是根据椭圆的对称性可知,四个焦点构成的四边形为菱形,面积![]() ,解得
,解得![]() ,可以得到椭圆
,可以得到椭圆![]() ,
,![]() ;(2)(i)本问考查圆锥曲线中的定点、定值问题,分析题意,设
;(2)(i)本问考查圆锥曲线中的定点、定值问题,分析题意,设![]() ,而
,而![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,于是
,于是![]() ,又因为
,又因为![]() ,代入上式易求
,代入上式易求![]() ;(ii)根据(i)问,可先证明
;(ii)根据(i)问,可先证明![]() 为定值,再证明
为定值,再证明![]() 为定值,于是可以得到
为定值,于是可以得到![]() 为定值,由于
为定值,由于![]() ,
,![]() ,所以可以得
,所以可以得![]() 为定值.
为定值.
试题解析:(1)依题意![]() ,设
,设![]() ,
,![]() ,由对称性,四个焦点构成的四边形为菱形,且面积
,由对称性,四个焦点构成的四边形为菱形,且面积![]() ,解得:
,解得:![]() .
.
所以椭圆![]() ,
,![]() .
.
(2)(i)设![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
所以:![]() .
.
直线![]() ,
,![]() 斜率之积为常数
斜率之积为常数![]() .
.
(ii)设![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,
所以:![]() ,同理:
,同理:![]() ,
,
所以:![]() ,由
,由![]() ,
,![]() ,结合(i)有
,结合(i)有
![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,直棱柱ABC﹣A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= ![]() AB. (Ⅰ)证明:BC1∥平面A1CD;
AB. (Ⅰ)证明:BC1∥平面A1CD;
(Ⅱ)求二面角D﹣A1C﹣E的余弦值.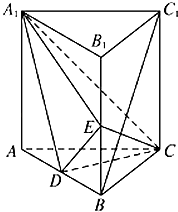
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点为极点,
为参数).以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生产甲乙两种元件,其质量按检测指标划分为:指标大于或者等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
元件甲 | 8 | 12 | 40 | 32 | 8 |
元件乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计元件甲、乙为正品的概率;
(2)生产一件元件甲,若是正品可盈利40元,若是次品则亏损5元,生产一件元件乙,若是正品可盈利50元,若是次品则亏损10元.在(1)的前提下:
(i)记![]() 为生产1件甲和1件乙所得的总利润,求随机变量
为生产1件甲和1件乙所得的总利润,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)求生产5件元件乙所获得的利润不少于140元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2+cx+d(a≠0)的对称中心为M(x0 , y0),记函数f(x)的导函数为f′(x),f′(x)的导函数为f″(x),则有f″(x0)=0.若函数f(x)=x3﹣3x2 , 则可求出f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(
)+f( ![]() )的值为( )
)的值为( )
A.4029
B.﹣4029
C.8058
D.﹣8058
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于两点
交于两点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(kx+4)lnx﹣x(x>1),若f(x)>0的解集为(s,t),且(s,t)中只有一个整数,则实数k的取值范围为( )
A.( ![]() ﹣2,
﹣2, ![]() ﹣
﹣ ![]() )
)
B.( ![]() ﹣2,
﹣2, ![]() ﹣
﹣ ![]() ]
]
C.( ![]() ﹣
﹣ ![]() ,
, ![]() ﹣1]
﹣1]
D.( ![]() ﹣
﹣ ![]() ,
, ![]() ﹣1)
﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com