
【题目】如图,四棱锥![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() ,点
,点![]() 在线段
在线段![]() ,
,![]() .
.
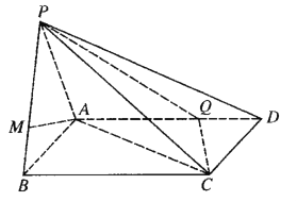
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)首先在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,根据已知条件得到
,根据已知条件得到![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,从而得到
,从而得到![]() ,四边形
,四边形![]() 是平行四边形,即
是平行四边形,即![]() ,再利用线面平行的判定即可证明.
,再利用线面平行的判定即可证明.
(2)首先取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,根据
,根据![]() ,得到
,得到![]() .利用面面垂直的性质得到
.利用面面垂直的性质得到![]() 平面
平面![]() ,从而得到
,从而得到![]() ,再利用线面垂直的性质即可证明
,再利用线面垂直的性质即可证明![]() 平面
平面![]() ,从而得到
,从而得到![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,再计算其正弦值即可.
所成的角,再计算其正弦值即可.
(1)在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,
,
如图所示: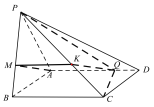
因为![]() ,所以
,所以![]() ,
,
所以![]() ,且
,且![]() .
.
又因为![]() ,所以
,所以![]() ,且
,且![]() .
.
所以![]() ,四边形
,四边形![]() 是平行四边形,所以
是平行四边形,所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,如图所示:
,如图所示:
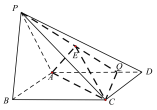
因为![]() ,则
,则![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
即![]() ,所以
,所以![]() .
.
又因为平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
因为![]() ,
,
![]() .
.


科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图(如图①)、90后从事互联网行业岗位分布条形图(如图②),则下列结论中不一定正确的是( )


注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知![]() ,
,![]() ,
,![]() 、
、![]() 分別为
分別为![]() 、
、![]() 的中点
的中点![]() ,将
,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,
,![]() 为
为![]() 的中点.
的中点.
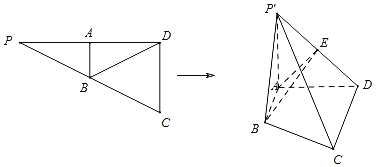
(1)证明:![]() 平面
平面![]() ;
;
(2)当正视图方向与向量![]() 的方向相同时,
的方向相同时,![]() 的正视图为直角三角形,求此时二面角
的正视图为直角三角形,求此时二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒蔓延以来,世界各国都在研制疫苗,某专家认为,某种抗病毒药品对新型冠状病毒具有抗病毒、抗炎作用,假如规定每天早上7:00和晚上7:00各服药一次,每次服用该药药量700毫克具有抗病毒功效,若人的肾脏每12小时从体内滤出这种药的70%,该药在人体内含量超过1000毫克,就将产生副作用,若人长期服用这种药,则这种药__________(填“会”或者“不会”)对人体产生副作用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 为椭圆上任意一点,当
为椭圆上任意一点,当![]() 时,
时,![]() 的面积为
的面积为![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经点
经点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() ,两个焦点分别为
,两个焦点分别为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() 的内切圆半径为
的内切圆半径为![]() ,求以
,求以![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com