
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如表:
x | ﹣ |
|
|
|
|
|
|
y | ﹣1 | 1 | 3 | 1 | ﹣1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果:
( i)当x∈[0, ![]() ]时,方程f(3x)=m恰有两个不同的解,求实数m的取值范围;
]时,方程f(3x)=m恰有两个不同的解,求实数m的取值范围;
( ii)若α,β是锐角三角形的两个内角,试比较f(sinα)与f(cosβ)的大小.
【答案】
(1)解:设f(x)的最小正周期为T,则由表格可得T= ![]() ﹣(﹣
﹣(﹣ ![]() )=2π=
)=2π= ![]() ,得ω=1,
,得ω=1,
再根据 ![]() ,解得
,解得 ![]() ,
,
再根据五点法作图,可得令ω ![]() +φ=
+φ= ![]() ,即
,即 ![]() +φ=
+φ= ![]() ,解得φ=﹣
,解得φ=﹣ ![]() ,
,
∴f(x)=2sin(x﹣ ![]() )+1.
)+1.
(2)解:( i)f(3x)=2sin(3x﹣ ![]() )+1,令t=3x﹣
)+1,令t=3x﹣ ![]() ,∵x∈[0,
,∵x∈[0, ![]() ],∴t∈[﹣
],∴t∈[﹣ ![]() ,
, ![]() ],
],
如图,s=sint 在[﹣ ![]() ,
, ![]() ]上有两个不同的解,则s∈[
]上有两个不同的解,则s∈[ ![]() ,1),
,1),
∴方程 f(3x)=2sin(3x﹣ ![]() )+1=2s+1=m在x∈[0,
)+1=2s+1=m在x∈[0, ![]() ]时恰好有两个不同的解,则m∈[
]时恰好有两个不同的解,则m∈[ ![]() +1,3),
+1,3),
即实数m的取值范围是[ ![]() +1,3).
+1,3).
( ii)由 ![]() 得
得 ![]() ,
,
∴f(x)在 ![]() 上单调递增,故在[0,1]上单调递增.
上单调递增,故在[0,1]上单调递增.
∵α、β是锐角三角形的两个内角,∴α+β> ![]() ,
, ![]() >α>
>α> ![]() ﹣β,
﹣β,
∴sinα>sin( ![]() ﹣β)=cosβ,且sinα,cosβ∈[0,1],于是f(sinα)>f(cosβ).
﹣β)=cosβ,且sinα,cosβ∈[0,1],于是f(sinα)>f(cosβ).
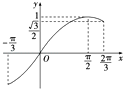
【解析】(1)由函数的最值求出A、B,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.(2)( i)由题意可得y=2sin(3x﹣ ![]() )+1的图象和直线y=m在[0,
)+1的图象和直线y=m在[0, ![]() ]上恰好有两个不同的交点,数形结合求得m的范围;( ii)由条件可得f(x)在
]上恰好有两个不同的交点,数形结合求得m的范围;( ii)由条件可得f(x)在 ![]() 上单调递增,故在[0,1]上单调递增,且α、β是锐角三角形的两个内角,α+β>
上单调递增,故在[0,1]上单调递增,且α、β是锐角三角形的两个内角,α+β> ![]() ,即
,即 ![]() >α>
>α> ![]() ﹣β,由此可得f(sinα)与f(cosβ)的大小关系.
﹣β,由此可得f(sinα)与f(cosβ)的大小关系.
【考点精析】认真审题,首先需要了解五点法作函数y=Asin(ωx+φ)的图象(描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线)).


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】某市举办校园足球赛,组委会为了做好服务工作,招募了12名男志愿者和10名女志愿者,调查发现男女志愿者中分别有8人和4人喜欢看足球比赛,其余不喜欢
(1)根据以上数据完成以下2×2列联表:
喜欢看足球比赛 | 不喜欢看足球比赛 | 总计 | |
男 | |||
女 | |||
总计 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜欢看足球比赛有关?
(3)从女志愿者中抽取2人参加某场足球比赛服务工作,若其中喜欢看足球比赛的人数为ξ,求ξ的分布列和数学期望.
附:参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
参考数据:
P(K2≥k0) | 0.4 | 0.25 | 0.10 | 0.010 |
k0 | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 上的一个动点,弦
上的一个动点,弦![]() 分别过左右焦点
分别过左右焦点![]() ,且当线段
,且当线段![]() 的中点在
的中点在![]() 轴上时,
轴上时, ![]() .
.
(1)求该椭圆的离心率;(2)设![]() ,试判断
,试判断![]() 是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
是否为定值?若是定值,求出该定值,并给出证明;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点. 
(1)求证:BD1∥平面A1DE;
(2)求直线A1E与平面AD1E所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解一个英语教改实验班的情况,举行了一次测试,将该班30位学生的英语成绩进行统计,得图示频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 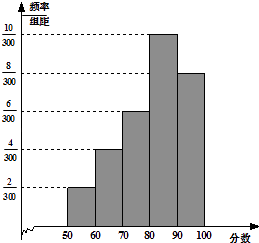
(1)求出该班学生英语成绩的众数,平均数及中位数;
(2)从成绩低于80分的学生中随机抽取2人,规定抽到的学生成绩在[50,60)的记1绩点分,在[60,80)的记2绩点分,设抽取2人的总绩点分为ξ,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnax﹣ ![]() (a≠0).
(a≠0).
(1)求此函数的单调区间及最值;
(2)求证:对于任意正整数n,均有1+ ![]() +
+ ![]() …+
…+ ![]() ≥ln
≥ln ![]() (e为自然对数的底数).
(e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为16分)设A,B分别为椭圆![]()
![]() 的左、右顶点,椭圆的长轴长为
的左、右顶点,椭圆的长轴长为![]() ,且点
,且点![]() 在该椭圆上.
在该椭圆上.
(1)求椭圆的方程;
(2)设![]() 为直线
为直线![]() 上不同于点
上不同于点![]() 的任意一点,若直线
的任意一点,若直线![]() 与椭圆相交于异于
与椭圆相交于异于![]() 的点
的点![]() ,证明:△
,证明:△![]() 为钝角三角形.
为钝角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号001,002,…,699,700.从中抽取70个样本,如图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第5个样本编号是( ) 
A.607
B.328
C.253
D.007
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com