巳知⊙C的方程为(x-1)2+(y-1)2=1,直线L:4x+3y+m=0(其中m<-2)与x、y轴的正半轴分别相交于A、B两点,点P(x,y)(xy>0)是线段AB上动点,如果直线L与圆C相切,则m的值等于________;log3x+log3y的最大值等于________.
-12 1
分析:由圆的方程找出圆心坐标和圆的半径r,根据直线l与圆C相切,得到圆心到直线l的距离等于圆的半径,列出关于m的方程,求出方程的解即可得到m的值;
由求出的m的值代入直线l的方程确定出直线l,然后用含x的式子表示出y,把表示出的y代入xy得到一个二次函数,然后利用二次函数求最值的方法求出xy的最大值,然后利用对数函数的运算法则把所求的式子化简后,根据3大于1得到对数函数为增函数,把xy的最大值代入即可求出所求式子的最大值.
解答:由圆的方程得到圆心C(1,1),半径r=1,
因为直线l与圆C相切,所以圆心到直线l的距离d=r=1,即
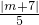
=1,
解得:m=-2(与已知m<-2矛盾,舍去)或m=-12,
所以满足题意的m的值为-12;
由3>1,得到对数函数为增函数,
由4x+3y-12=0,得到y=-

x+4,所以xy=-

x
2+4x,
当x=-
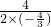
即x=

>0,y=2>0时,xy的最大值为3,
则log
3x+log
3y的最大值为log
3xy=log
33=1.
故答案为:-12;1.
点评:此题考查学生掌握直线与圆相切时满足的条件,灵活运用点到直线的距离公式化简求值,掌握二次函数求最大值的方法,是一道中档题.

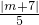 =1,
=1, x+4,所以xy=-
x+4,所以xy=- x2+4x,
x2+4x,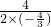 即x=
即x= >0,y=2>0时,xy的最大值为3,
>0,y=2>0时,xy的最大值为3,




