
【题目】南充高中扎实推进阳光体育运动,积极引导学生走向操场,走进大自然,参加体育锻炼,每天上午第三节课后全校大课间活动时长35分钟.现为了了解学生的体育锻炼时间,采用简单随机抽样法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下表:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计我校7000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人;
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男生和女生各1人的概率.
【答案】(1)700人;(2) ①男生抽取4人,女生抽取1人.② ![]()
【解析】
(1)100名学生中“锻炼达人”的人数为10人,由此能求出7000名学生中“锻炼达人”的人数.
(2)①100名学生中的“锻炼达人”有10人,其中男生8人,女生2人.从10人中按性别分层抽取5人参加体育活动,能求出男生,女生各抽取多少人.
②抽取的5人中有4名男生和1名女生,四名男生一次编号为男1,男2,男3,男4,5人中随机抽取2人,利用列举法能求出抽取的2人中男生和女生各1人的概率.
(1)由表可知,100名学生中“锻炼达人”的人数为10人,将频率视为概率,我校7000名学生中“锻炼达人”的人数为![]() (人)
(人)
(2)①由(1)知100名学生中的“锻炼达人”有10人,其中男生8人,女生2人.
从10人中按性别分层抽取5人参加体育活动,则男生抽取4人,女生抽取1人.
②抽取的5人中有4名男生和1名女生,四名男生一次编号为男1,男2,男3,男4,则5人中随机抽取2人的所有结果有:男1男2,男1男3,男1 男4,男1女,男2男3,男2男4,男2女,男3男4,男3女,男4女.共有10种结果,且每种结果发生的可能性相等.记“抽取的2人中男生和女生各1人”为事件A,则事件A包含的结果有男1女,男2女,男3女,男4女,共4个,故![]() .
.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:
【题目】在![]() 年
年![]() 月
月![]() 日,某市物价部门对本市的
日,某市物价部门对本市的![]() 家商场的某商品的一天销售量及其价格进行调查,
家商场的某商品的一天销售量及其价格进行调查,![]() 家商场的售价
家商场的售价![]() 元和销售量
元和销售量![]() 件之间的一组数据如表所示:
件之间的一组数据如表所示:
价格 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量 | 11 | 10 | 8 | 6 | 5 |
根据公式计算得相关系数![]() ,其线性回归直线方程是:
,其线性回归直线方程是:![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
参考:![]()
A.有![]() 的把握认为变量
的把握认为变量![]() 具有线性相关关系
具有线性相关关系
B.回归直线恒过定点![]()
C.![]()
D.当![]() 时,
时,![]() 的估计值为
的估计值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的偶函数,对于任意
上的偶函数,对于任意![]() ,都有
,都有![]() 成立,当
成立,当![]() 时,有
时,有![]() 给出下列命题:
给出下列命题:
①![]() ;
;
②函数![]() 的周期是6;
的周期是6;
③函数![]() 在
在![]() 上为增函数;
上为增函数;
④函数![]() 在
在![]() 上有四个零点.
上有四个零点.
其中所有正确命题的序号为_______________.(把所有正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小李从网上购买了一件商品,快递员计划在下午5:00-6:00之间送货上门,已知小李下班到家的时间为下午5:30-6:00.快递员到小李家时,如果小李未到家,则快递员会电话联系小李.若小李能在10分钟之内到家,则快递员等小李回来;否则,就将商品存放在快递柜中.则小李需要去快递柜收取商品的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() ,在某一周期内的图象时,列表并填入了部分数据,如下表:
,在某一周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,并求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“互联网![]() ”是“智慧城市”的重要内士,
”是“智慧城市”的重要内士,![]() 市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费
市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费![]() .为了解免费
.为了解免费![]() 在
在![]() 市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了
市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了![]() 人进行抽样分析,得到如下列联表(单位:人):
人进行抽样分析,得到如下列联表(单位:人):
经常使用免费WiFi | 偶尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,判断是否有![]() 的把握认为
的把握认为![]() 市使用免费
市使用免费![]() 的情况与年龄有关;
的情况与年龄有关;
(2)将频率视为概率,现从该市![]() 岁以上的市民中用随机抽样的方法每次抽取
岁以上的市民中用随机抽样的方法每次抽取![]() 人,共抽取
人,共抽取![]() 次.记被抽取的
次.记被抽取的![]() 人中“偶尔或不用免费
人中“偶尔或不用免费![]() ”的人数为
”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,数学期望
的分布列,数学期望![]() 和方差
和方差![]() .
.
附: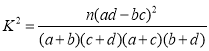 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数f(x),其导函数![]() ,当x≥0时,恒有
,当x≥0时,恒有![]()
![]() +f(﹣x)<0,若g(x)=x2f(x),则不等式g(x)<g(1﹣2x)的解集为( )
+f(﹣x)<0,若g(x)=x2f(x),则不等式g(x)<g(1﹣2x)的解集为( )
A.(![]() ,1)B.(﹣∞,
,1)B.(﹣∞,![]() )∪(1,+∞)
)∪(1,+∞)
C.(![]() ,+∞)D.(﹣∞,
,+∞)D.(﹣∞,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com