
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性.
的单调性.
(2)试问是否存在![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)见解析;(2) 存在;![]() 的取值范围为
的取值范围为![]() .
.
【解析】
(1)![]() ,
,![]() ,
,
所以![]() 得
得![]() ,所以通过对
,所以通过对![]() 与
与![]() 的大小关系进行分类讨论得
的大小关系进行分类讨论得![]() 的单调性;
的单调性;
(2)假设存在满足题意的![]() 的值,由题意需
的值,由题意需![]() ,所以由(1)的单调性求
,所以由(1)的单调性求![]() 即可;
即可;
又因为![]() 对
对![]() 恒成立,所以可以考虑从区间
恒成立,所以可以考虑从区间![]() 内任取一个
内任取一个![]() 值代入,解出
值代入,解出![]() 的取值范围,从而将
的取值范围,从而将![]() 的范围缩小减少讨论.
的范围缩小减少讨论.
解:(1)![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增
上单调递增
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增.
上单调递增.
(2)假设存在![]() ,使得
,使得![]() 对
对![]() 恒成立.
恒成立.
则![]() ,即
,即![]() ,
,
设![]() ,则存在
,则存在![]() ,使得
,使得![]() ,
,
因为![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,所以
,所以![]() 时
时![]() 即
即![]() .
.
又因为![]() 对
对![]() 恒成立时,需
恒成立时,需![]() ,
,
所以由(1)得:
当![]() 时,
时,![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
且![]() 成立,从而
成立,从而![]() 满足题意.
满足题意.
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() ,
,![]() 上单调递增,
上单调递增,
所以
所以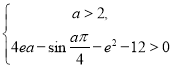 (*)
(*)
设![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,
,
所以![]() 的零点小于2,从而不等式组(*)的解集为
的零点小于2,从而不等式组(*)的解集为![]() ,
,
所以![]() 即
即![]() .
.
综上,存在![]() ,使得
,使得![]() 对
对![]() 恒成立,且
恒成立,且![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在![]() 地正西方向
地正西方向![]() 的
的![]() 处和正东方向
处和正东方向![]() 的
的![]() 处各一条正北方向的公路
处各一条正北方向的公路![]() 和
和![]() ,现计划在
,现计划在![]() 和
和![]() 路边各修建一个物流中心
路边各修建一个物流中心![]() 和
和![]() .
.
(1)若在![]() 处看
处看![]() ,
,![]() 的视角
的视角![]() ,在
,在![]() 处看
处看![]() 测得
测得![]() ,求
,求![]() ,
,![]() ;
;
(2)为缓解交通压力,决定修建两条互相垂直的公路![]() 和
和![]() ,设
,设![]() ,公路
,公路![]() 的每千米建设成本为
的每千米建设成本为![]() 万元,公路
万元,公路![]() 的每千米建设成本为
的每千米建设成本为![]() 万元.为节省建设成本,试确定
万元.为节省建设成本,试确定![]() ,
,![]() 的位置,使公路的总建设成本最小.
的位置,使公路的总建设成本最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
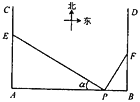
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 为正方形,且
为正方形,且![]() .若四棱锥
.若四棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,则球
的球面上,则球![]() 的表面积的最小值为_____;当四棱锥
的表面积的最小值为_____;当四棱锥![]() 的体积取得最大值时,二面角
的体积取得最大值时,二面角![]() 的正切值为_______.
的正切值为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻折成△![]() DE,使平面
DE,使平面![]() DE⊥平面BCDE,若M为线段
DE⊥平面BCDE,若M为线段![]() C的中点,下面四个命题中不正确的是( )
C的中点,下面四个命题中不正确的是( )
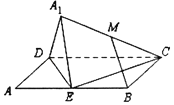
A.BM![]() 平面
平面![]() DEB.CE⊥平面
DEB.CE⊥平面![]() DE
DE
C.DE![]() BMD.平面
BMD.平面![]() CD⊥平面
CD⊥平面![]() CE
CE
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凤鸣山中学的高中女生体重![]() (单位:kg)与身高
(单位:kg)与身高![]() (单位:cm)具有线性相关关系,根据一组样本数据
(单位:cm)具有线性相关关系,根据一组样本数据![]() (
(![]() ),用最小二乘法近似得到回归直线方程为
),用最小二乘法近似得到回归直线方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.![]() 与
与![]() 具有正线性相关关系
具有正线性相关关系
B.回归直线过样本的中心点![]()
C.若该中学某高中女生身高增加1cm,则其体重约增加0.85kg
D.若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).

(1)根据以上数据完成下列![]() 列联表:
列联表:
主食蔬菜 | 主食肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否有99%的把握认为其亲属的饮食习惯与年龄有关?并写出简要分析.
参考公式和数据: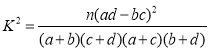 ,
,![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com