
如图,某生态园欲把一块四边形地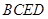 辟为水果园,其中
辟为水果园,其中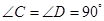 ,
,
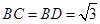 ,
,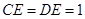 .若经过
.若经过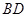 上一点
上一点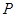 和
和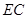 上一点
上一点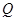 铺设一条道路
铺设一条道路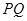 ,且
,且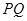 将四边形
将四边形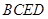 分成面积相等的两部分,设
分成面积相等的两部分,设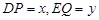 .
.
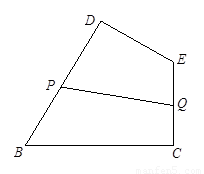
(1)求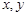 的关系式;
的关系式;
(2)如果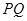 是灌溉水管的位置,为了省钱,希望它最短,求
是灌溉水管的位置,为了省钱,希望它最短,求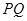 的长的最小值;
的长的最小值;
(3)如果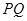 是参观路线,希望它最长,那么
是参观路线,希望它最长,那么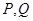 的位置在哪里?
的位置在哪里?
(1)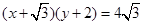 ;(2)
;(2)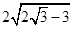 ;(3)P点在B处,Q点在E处.
;(3)P点在B处,Q点在E处.
【解析】
试题分析:(1)由题目条件可求出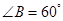 ,延长BD、CE交于点A,则由得出结论
,延长BD、CE交于点A,则由得出结论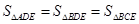 ,于是可知
,于是可知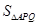 的面积,而它的面积又可用
的面积,而它的面积又可用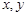 表示出来,于是问题得到解决;(2)
表示出来,于是问题得到解决;(2)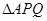 中利用余弦定理,可将
中利用余弦定理,可将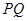 的长度用
的长度用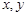 表示,再利用(1)的结果消去
表示,再利用(1)的结果消去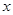 ,则得到
,则得到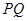 关于
关于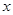 的函数关系式,然后利用基本不等式或求函数最值的一般方法求出函数的最小值或最大值,要注意函数的定义域;(3)思路同(2).
的函数关系式,然后利用基本不等式或求函数最值的一般方法求出函数的最小值或最大值,要注意函数的定义域;(3)思路同(2).
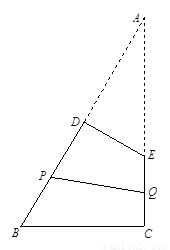
试题解析:(1)易知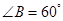 ,延长BD、CE交于点A,则
,延长BD、CE交于点A,则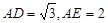 ,则
,则 .
.
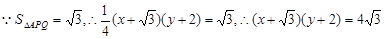 .
4分
.
4分
(2)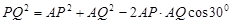
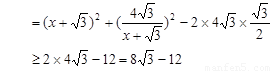 6分
6分
当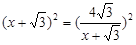 ,即
,即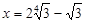 时,
时,
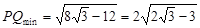 .
8分
.
8分
(3)令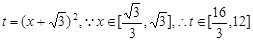 , 10分
, 10分
则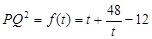 ,
,
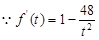 ,令
,令 得,
得,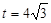 ,
12分
,
12分
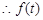 在
在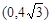 上是减函数,在
上是减函数,在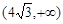 上是增函数,
上是增函数,
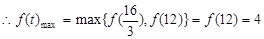 ,PQmax = 2,
14分
,PQmax = 2,
14分
此时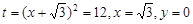 ,P点在B处,Q点在E处.
16分
,P点在B处,Q点在E处.
16分
考点:函数的应用、基本不等式、函数的最值.


科目:高中数学 来源: 题型:
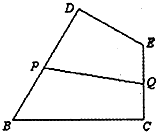 如图,某生态园欲把一块四边形地BCED辟为水果园,其中∠C=∠D=90°,BC=BD=
如图,某生态园欲把一块四边形地BCED辟为水果园,其中∠C=∠D=90°,BC=BD=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com