
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,直线
,直线![]() :
:![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动,![]() 是线段
是线段![]() 与
与![]() 轴的交点,动点
轴的交点,动点![]() 满足:
满足:![]() ,
,![]() .
.
(1)求动点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线与曲线
的垂线与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的最大值.
的最大值.
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】安徽怀远石榴(Punicagranatum)自古就有“九州之奇树,天下之名果”的美称,今年又喜获丰收.怀远一中数学兴趣小组进行社会调查,了解到某石榴合作社为了实现![]() 万元利润目标,准备制定激励销售人员的奖励方案:在销售利润超过
万元利润目标,准备制定激励销售人员的奖励方案:在销售利润超过![]() 万元时,按销售利润进行奖励,且奖金
万元时,按销售利润进行奖励,且奖金![]() (单位:万元)随销售利润
(单位:万元)随销售利润![]() (单位:万元)的增加而增加,但奖金总数不超过
(单位:万元)的增加而增加,但奖金总数不超过![]() 万元,同时奖金不能超过利润的
万元,同时奖金不能超过利润的![]() .同学们利用函数知识,设计了如下函数模型,其中符合合作社要求的是( )(参考数据:
.同学们利用函数知识,设计了如下函数模型,其中符合合作社要求的是( )(参考数据:![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次电影展,有14部参赛影片,组委会分两天在某一影院播映这14部电影,每天7部,其中有2部4D电影要求不在同一天放映,下列不能作为排片方案数的计算式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
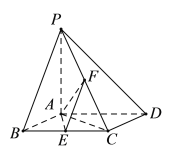
(I)证明:AE⊥PD;
(II)设AB=PA=2,
①求异面直线PB与AD所成角的正弦值;
②求二面角E-AF-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆C上,且
在椭圆C上,且![]() ⊥
⊥![]()
![]() ,△F1MF2的面积为
,△F1MF2的面积为![]() .
.
(1)求椭圆C的标准方程;
(2)已知直线l与椭圆C交于A,B两点,![]() ,若直线l始终与圆
,若直线l始终与圆![]() 相切,求半径r的值.
相切,求半径r的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直线![]() 垂直于
垂直于![]() 轴,与椭圆
轴,与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上,
上,![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,与曲线
,与曲线![]() 相切于点
相切于点![]() ,
,![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() ,点
,点![]() .
.
(1)求点P与抛物线C的焦点F的距离;
(2)设斜率为l的直线l与抛物线C交于A,B两点若△PAB的面积为![]() ,求直线l的方程;
,求直线l的方程;
(3)是否存在定圆M: ![]() ,使得过曲线C上任意一点Q作圆M的两条切线,与曲线C交于另外两点A,B时,总有直线AB也与圆M相切?若存在,求出m的值;若不存在,请说明理由.
,使得过曲线C上任意一点Q作圆M的两条切线,与曲线C交于另外两点A,B时,总有直线AB也与圆M相切?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com