
【题目】如图,在五棱锥P-ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.
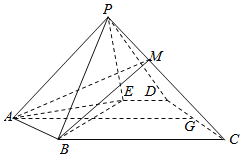
(Ⅰ)求证:平面PBE⊥平面APG;
(Ⅱ)已知AB=2,BC=![]() ,侧棱PA与底面ABCDE所成角为45°,S△PBE=
,侧棱PA与底面ABCDE所成角为45°,S△PBE=![]() ,点M在侧棱PC上,CM=2MP,求二面角M-AB-D的余弦值.
,点M在侧棱PC上,CM=2MP,求二面角M-AB-D的余弦值.
【答案】(I)见解析; (II)![]() .
.
【解析】
(Ⅰ)由题易证BE⊥PO,BE⊥AG,可得BE⊥平面PAG,既而证得平面PBE⊥平面APG;
(II)建立空间直角坐标系,分别求出平面MAB和平面ABD的法向量,再根据二面角的公式求得二面角M-AB-D的余弦值即可.
(Ⅰ)取BE中点F,连接AF,GF,由题意得A,F,G三点共线,
过点P作PO⊥AG于O,则PO⊥底面ABCDE
∵BE平面ABCDE,∴BE⊥PO,
∵△ABE是等边三角形,
∴BE⊥AG
∵AG∩PO=O,∴BE⊥平面PAG,
∵BE平面PBE,
∴平面PBE⊥平面APG.
(II)连接PF,∵![]()
又∵∠PAF=45°,∴PF⊥AF,∴PF⊥AF,
∴PF⊥底面ABCDE.
∴O点与F点重合.
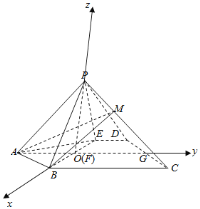
如图,以O为原点,分别以![]() 的方向为x轴,y轴,z轴正方向,建立空间直角坐标系.
的方向为x轴,y轴,z轴正方向,建立空间直角坐标系.
底面ABCDE的一个法向量![]()
∵![]() ,∴
,∴![]() ,
,
设平面ABM的法向量![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴ ,取
,取![]() 则
则![]() ,
,
∴![]() ,
,
∵二面角的法向量![]() 分别指向二面角的内外,<
分别指向二面角的内外,<![]() >即为二面角的平面角,
>即为二面角的平面角,
∴cos<![]() >
>![]() =
=![]() =
=![]() .
.
∴二面角M-AB-D的余弦值为![]() .
.
)


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() 、
、![]() ,左右顶点分别是
,左右顶点分别是![]() 、
、![]() ,长轴长为
,长轴长为![]() ,
,![]() 是以原点为圆心,
是以原点为圆心,![]() 为半径的圆的任一条直径,四边形
为半径的圆的任一条直径,四边形![]() 的面积最大值为
的面积最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)不经过原点的直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,
两点,
①若直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
②若直线![]() 的斜率是直线
的斜率是直线![]() 、
、![]() 斜率的等比中项,求
斜率的等比中项,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 截直线
截直线![]() 所得的线段的长度为
所得的线段的长度为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,DC⊥平面ABC,![]() ,
,![]() ,
,![]() ,P、Q分别为AE,AB的中点.
,P、Q分别为AE,AB的中点.
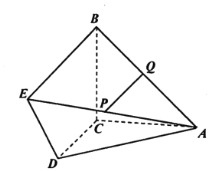
(1)证明:![]() 平面
平面![]() .
.
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)求平面![]() 与平面
与平面![]() 所成锐二面角的大小。
所成锐二面角的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为中心,以坐标轴为对称轴的帮圆C经过点M(2,1),N .
.
(1)求椭圆C的标准方程;
(2)经过点M作倾斜角互补的两条直线,分别与椭圆C相交于异于M点的A,B两点,当△AMB面积取得最大值时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]()
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 作动直线
作动直线![]() 的平行线交轨迹
的平行线交轨迹![]() 于
于![]() 两点,则
两点,则![]() 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,设椭圆
中,设椭圆![]() 的左焦点为
的左焦点为![]() ,左准线为
,左准线为![]() 为椭圆
为椭圆![]() 上任意一点,直线
上任意一点,直线![]() ,垂足为
,垂足为![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.
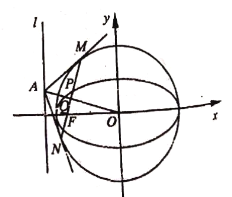
(1)若![]() ,且
,且![]() ,直线
,直线![]() 的方程为
的方程为![]() .①求椭圆
.①求椭圆![]() 的方程;②是否存在点
的方程;②是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求证:直线
两点,求证:直线![]() 均与圆
均与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知抛物线的焦点F在y轴上,其准线与双曲线![]()
![]() 的下准线重合.
的下准线重合.

(1)求抛物线的标准方程;
(2)设A(![]() ,
,![]() )(
)(![]() >0)是抛物线上一点,且AF=
>0)是抛物线上一点,且AF=![]() ,B是抛物线的准线与y轴的交点.过点A作抛物线的切线l,过点B作l的平行线l′,直线l′与抛物线交于点M,N,求△AMN的面积.
,B是抛物线的准线与y轴的交点.过点A作抛物线的切线l,过点B作l的平行线l′,直线l′与抛物线交于点M,N,求△AMN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}为等差数列,a7﹣a2=10,且a1,a6,a21依次成等比数列.
(1)求数列{an}的通项公式;
(2)设bn![]() ,数列{bn}的前n项和为Sn,若Sn
,数列{bn}的前n项和为Sn,若Sn![]() ,求n的值.
,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com