
(1)��C�ķ���Ϊ![]() +
+![]() =1,n=3,��P1(10��0)��S3=255�����P3�����ꣻ(ֻ��д��һ��)
=1,n=3,��P1(10��0)��S3=255�����P3�����ꣻ(ֻ��д��һ��)
(2)��C�ķ���Ϊ![]() +
+![]() =1(a��b��0)����P1(a��0)�����ڸ�������Ȼ��n��������d�仯ʱ����Sn����Сֵ��
=1(a��b��0)����P1(a��0)�����ڸ�������Ȼ��n��������d�仯ʱ����Sn����Сֵ��
(3)��ѡ��һ������Բ��Ķ�������C��C��һ��P1�����ڸ�������Ȼ��n��д�����������ĵ�P1��P2������Pn���ڵij�Ҫ��������˵������.
22.[��] (1) a1=|OP1|2=100,
��S3=![]() (a1+a3)=255,��a3=|OP3|2=70.
(a1+a3)=255,��a3=|OP3|2=70.
��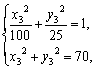 ���
���
���P3���������Ϊ(2![]() ��
��![]() ).
).
(2)[�ⷨһ]ԭ��O����������C��![]() +
+![]() =1(a��b��0)�ϸ������С����Ϊb��������Ϊa.
=1(a��b��0)�ϸ������С����Ϊb��������Ϊa.
��a1=|OP1|2=a2,��d��0����an=|OPn|2=a2+(n��1)d��b2.
��![]() ��d��0.
��d��0.
��n��3,![]() ��0,
��0,
��Sn=na2+![]() d�ڣ�
d�ڣ�![]() ,0)�ϵ���.
,0)�ϵ���.
��Sn����СֵΪna2+![]() ��
��![]() =
=![]() .
.
[�ⷨ��]��ÿ����Ȼ��k(2��k��n),
��
���yk2=![]() .
.
��0��yk2��b2,��![]() ��d��0,��
��d��0,��![]() ��d��0.
��d��0.
������ⷨһ��ͬ.
(3)[�ⷨһ]��˫����C��![]() ��
��![]() =1����P1(a,0),
=1����P1(a,0),
����ڸ�����n����P1��P2������Pn���ڵij�Ҫ������d��0.
��ԭ��O��˫����C�ϸ���ľ���h�ʣ�|a|,+��)����|OP1|2=a2,
���P1��P2������Pn���ڵ��ҽ���|OPn|2��|OP1|2����d��0.
[�ⷨ��]��������C��y2=2px,��P1(0,0)������ڸ�����n��
��P1��P2����,Pn���ڵij�Ҫ������d��0.����ͬ��.
[�ⷨ��]��ԲC��(x��a)2+y2=a2(a��0),��P1(0��0)��
����ڸ�����n,��P1��P2������Pn���ڵij�Ҫ������0��d��![]() .
.
��ԭ��O��ԲC�ϸ������С����Ϊ0��������Ϊ2|a|,��|OP1|2=0��
��d��0��|OPn|2=(n��1)d��4a2,
��0��d��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��04���Ϻ�������(18��)
��P1(x1,y1), P1(x2,y2),��, Pn(xn,yn)(n��3,n��N) �Ƕ�������C�ϵĵ�, ��a1=![]() 2, a2=
2, a2=![]() 2, ��, an=
2, ��, an=![]() 2������һ������Ϊd(d��0) �ĵȲ�����, ����O������ԭ��. ��Sn=a1+a2+��+an.
2������һ������Ϊd(d��0) �ĵȲ�����, ����O������ԭ��. ��Sn=a1+a2+��+an.
(1) ��C�ķ���Ϊ![]() =1,n=3. ��P1(3,0) ��S3=255, ���P3�����ꣻ
=1,n=3. ��P1(3,0) ��S3=255, ���P3�����ꣻ
(ֻ��д��һ��)
(2)��C�ķ���Ϊ![]() (a>b>0). ��P1(a,0), ���ڸ�������Ȼ��n, ������d�仯ʱ, ��Sn����Сֵ��
(a>b>0). ��P1(a,0), ���ڸ�������Ȼ��n, ������d�仯ʱ, ��Sn����Сֵ��
. (3)��ѡ��һ������Բ��Ķ�������C��C�ϵ�һ��P1,���ڸ�������Ȼ��n,д�����������ĵ�P1, P2,��Pn���ڵij�Ҫ����,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��04���Ϻ����ģ�(18��)
��P1(x1,y1), P1(x2,y2),��, Pn(xn,yn)(n��3,n��N) �Ƕ�������C�ϵĵ�, ��a1=![]() 2, a2=
2, a2=![]() 2, ��, an=
2, ��, an=![]() 2������һ������Ϊd(d��0) �ĵȲ�����, ����O������ԭ��. ��Sn=a1+a2+��+an.
2������һ������Ϊd(d��0) �ĵȲ�����, ����O������ԭ��. ��Sn=a1+a2+��+an.
(1) ��C�ķ���Ϊ![]() ��y2=1,n=3. ��P1(3,0) ��S3=162, ���P3�����ꣻ
��y2=1,n=3. ��P1(3,0) ��S3=162, ���P3�����ꣻ
(ֻ��д��һ��)
(2) ��C�ķ���Ϊy2=2px(p��0). ��P1(0,0), ���ڸ�������Ȼ��n, ֤����
(x1+p)2, (x2+p)2, ��,(xn+p)2�ɵȲ����У�
(3) ��C�ķ���Ϊ![]() (a>b>0). ��P1(a,0), ���ڸ�������Ȼ��n, ������d�仯ʱ, ��Sn����Сֵ.
(a>b>0). ��P1(a,0), ���ڸ�������Ȼ��n, ������d�仯ʱ, ��Sn����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
(1)��C�ķ���Ϊ![]() =1,n=3,��P1(10��0)��S3=255�����P3�����ꣻ(ֻ��д��һ��)
=1,n=3,��P1(10��0)��S3=255�����P3�����ꣻ(ֻ��д��һ��)
(2)��C�ķ���Ϊ![]() +
+![]() =1(a��b��0)����P1(a,0)�����ڸ�������Ȼ��n��������d�仯ʱ����Sn����Сֵ.
=1(a��b��0)����P1(a,0)�����ڸ�������Ȼ��n��������d�仯ʱ����Sn����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
(1)��C�ķ���Ϊ![]() ��y2=1,n=3,��P1(3��0)��S3=162�����P3�����ꣻ(ֻ��д��һ��)
��y2=1,n=3,��P1(3��0)��S3=162�����P3�����ꣻ(ֻ��д��һ��)
(2)��C�ķ���Ϊy2=2px(p��0)����P1(0��0),���ڸ�������Ȼ��n��֤����(x1+p)2,(x2+p)2,��,(xn+p)2�ɵȲ����У�
(3)��C�ķ���Ϊ![]() +
+![]() =1(a��b��0)����P1(a��0)�����ڸ�������Ȼ��n��������d�仯ʱ����Sn����Сֵ.
=1(a��b��0)����P1(a��0)�����ڸ�������Ȼ��n��������d�仯ʱ����Sn����Сֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com