
【题目】已知函数f(x)=﹣![]() sin2x+sinxcosx+
sin2x+sinxcosx+![]() ,x∈[0,
,x∈[0,![]() ]
]
(1)求函数f(x)的值域;
(2)若f(![]() )=
)=![]() ,α∈(0,π),求sinα的值.
,α∈(0,π),求sinα的值.
【答案】(1)[﹣1,1];(2)![]()
【解答】解:(1)f(x)=﹣![]() sin2x+sinxcosx+
sin2x+sinxcosx+![]()
=﹣![]() ×
×![]() +
+![]() sin2x+
sin2x+![]()
=![]() cos2x+
cos2x+![]() sin2x
sin2x
=sin(2x+![]() )
)
故f(x)值域为:[﹣1,1];
(2)∵f(![]() )=
)=![]() ,
,
∴sin(α+![]() )=
)=![]() ,
,
∵α∈(0,π),
∴α+![]() ∈(
∈(![]() ,
,![]() ),
),
则α+![]() 为钝角,
为钝角,
故cos(α+![]() )=﹣
)=﹣![]() ,
,
故sinα=sin[(α+![]() )﹣
)﹣![]() ]=sin(α+
]=sin(α+![]() )cos
)cos![]() ﹣cos(α+
﹣cos(α+![]() )sin
)sin![]() =
=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.
【解析】
试题(1)先根据二倍角公式以及配角公式将函数化为基本三角函数,再根据自变量范围确定正弦函数取值范围(2)先由f(![]() )=
)=![]() ,解得
,解得![]() ,由同角关系可得
,由同角关系可得![]() ,再根据
,再根据![]() ,利用两角差正弦公式求sinα的值
,利用两角差正弦公式求sinα的值
试题解析:解:(1)f(x)=﹣![]() sin2x+sinxcosx+
sin2x+sinxcosx+![]()
=﹣![]() ×
×![]() +
+![]() sin2x+
sin2x+![]()
=![]() cos2x+
cos2x+![]() sin2x
sin2x
=sin(2x+![]() )
)
故f(x)值域为:[﹣1,1];
(2)∵f(![]() )=
)=![]() ,
,
∴sin(α+![]() )=
)=![]() ,
,
∵α∈(0,π),
∴α+![]() ∈(
∈(![]() ,
,![]() ),
),
则α+![]() 为钝角,
为钝角,
故cos(α+![]() )=﹣
)=﹣![]() ,
,
故sinα=sin[(α+![]() )﹣
)﹣![]() ]=sin(α+
]=sin(α+![]() )cos
)cos![]() ﹣cos(α+
﹣cos(α+![]() )sin
)sin![]() =
=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人组成一个小组参加电视台举办的听曲猜歌名活动,在每一轮活动中,依次播放三首乐曲,然后甲猜第一首,乙猜第二首,丙猜第三首,若有一人猜错,则活动立即结束;若三人均猜对,则该小组进入下一轮,该小组最多参加三轮活动.已知每一轮甲猜对歌名的概率是![]() ,乙猜对歌名的概率是
,乙猜对歌名的概率是![]() ,丙猜对歌名的概率是
,丙猜对歌名的概率是![]() ,甲、乙、丙猜对与否互不影响.
,甲、乙、丙猜对与否互不影响.
(I)求该小组未能进入第二轮的概率;
(Ⅱ)记乙猜歌曲的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() .
.
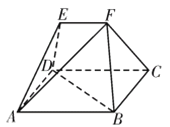
(1)过![]() 作截面与线段
作截面与线段![]() 交于点
交于点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并予以证明;
的位置,并予以证明;
(2)在(1)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①对立事件一定是互斥事件;②若A,B为两个随机事件,则P(A∪B)=P(A)+P(B);③若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A,B满足P(A)+P(B)=1,则A与B是对立事件.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线l:2x﹣y=0上,且与直线l1:x﹣y+1=0相切.
(Ⅰ)若圆C与圆x2+y2﹣2x﹣4y﹣76=0外切,试求圆C的半径;
(Ⅱ)满足已知条件的圆显然不只一个,但它们都与直线l1相切,我们称l1是这些圆的公切线.这些圆是否还有其他公切线?若有,求出公切线的方程,若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型高端制造公司为响应《中国制造2025》中提出的坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,准备加大产品研发投资,下表是该公司2017年5~12月份研发费用(百万元)和产品销量(万台)的具体数据:

(1)根据数据可知![]() 与
与![]() 之间存在线性相关关系
之间存在线性相关关系
(i)求出![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(ii)若2018年6月份研发投人为25百万元,根据所求的线性回归方程估计当月产品的销量;
(2)公司在2017年年终总结时准备从该年8~12月份这5个月中抽取3个月的数据进行重点分析,求没有抽到9月份数据的概率.
参考数据: ![]() ,
,![]() .
.
参考公式:对于一组数据![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 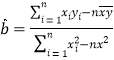 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() 为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.367 | 0.329 | 0.308 | 0.290 |
(I)现从抽取的6件合格产品中再任选3件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望;
的分布列和期望;
(II)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(i)根据所给统计量,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(ii)已知优等品的收益![]() (单位:千元)与
(单位:千元)与![]() 的关系为
的关系为![]() ,则当优等品的尺寸
,则当优等品的尺寸![]() 为何值时,收益
为何值时,收益![]() 的预报值最大? (精确到0.1)
的预报值最大? (精确到0.1)
附:对于样本![]() , 其回归直线
, 其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
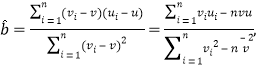
![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com